摘要:27. “5·12 四川汶川大地震的灾情牵动全国人民的心.某市A.B两个蔬菜基地得知四川C.D两个灾民安置点分别急需蔬菜240吨和260吨的消息后.决定调运蔬菜支援灾区.已知A蔬菜基地有蔬菜200吨.B蔬菜基地有蔬菜300吨.现将这些蔬菜全部调往C.D两个灾民安置点.从A地运往C.D两处的费用分别为每吨20元和25元.从B地运往C.D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨. (1) 请填写下表.并求两个蔬菜基地调运蔬菜的运费相等时x的值, C D 总计 A 200吨 B x吨 300吨 总计 240吨 260吨 500吨 (2) 设A.B两个蔬菜基地的总运费为w元.写出w与x之间的函数关系式.并求总运费最小的调运方案, (3) 经过抢修.从B地到C处的路况得到进一步改善.缩短了运输时间.运费每吨减少元(>0).其余线路的运费不变.试讨论总运费最小的调运方案. [命题意图]考查学生列方程解应用题. [参考答案] (1)填表 C D 总计 A (240-x)吨 (x-40)吨 200吨 B x吨 (300-x)吨 300吨 总计 240吨 260吨 500吨 依题意得:. ------------------------------4分 解得: . -----------------------------------------------------------------5分 (2) w与x之间的函数关系为:. -------------------------------------8分 依题意得: . ∴40≤≤240 ----------------------------------9分 在中.∵2>0. ∴随的增大而增大. 表一: C D A 200吨 0吨 B 40吨 260吨 故当=40时.总运费最小. ---------------------10分 此时调运方案为如右表一. ----------------------11分 (3)由题意知 ∴0<<2时.(2)中调运方案总运费最小,-----12分 C D A 0吨 200吨 B 240吨 60吨 =2时.在40≤≤240的前提下调运 表二: 方案的总运费不变, ------13分 2<<15时.=240总运费最小. 其调运方案如右表 [试题来源]初三月考试题改编
网址:http://m.1010jiajiao.com/timu_id_4425006[举报]
(本题满分14分,其中第(1)题4分,第(2)题的第?、?小题分别为4分、6分)
如图1,在△ABC中,已知AB=15,cosB=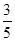 ,tanC=
,tanC=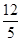 .点D为边BC上的动点(点D不与B、C重合),以D为圆心,BD为半径的⊙D交边AB于点E.
.点D为边BC上的动点(点D不与B、C重合),以D为圆心,BD为半径的⊙D交边AB于点E.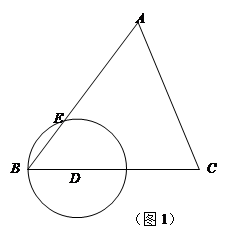
(1)设BD=x,AE=y,求 与
与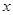 的函数关系式,并写出函数定域义;
的函数关系式,并写出函数定域义;
(2)如图2,点F为边AC上的动点,且满足BD=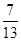 CF,联结DF.
CF,联结DF.
①当△ABC和△FDC相似时,求⊙D的半径;
② 当⊙D与以点F为圆心,FC为半径⊙F外切时,求⊙D的半径.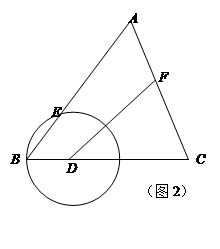
(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)在Rt△ABC中,∠ACB=90°,BC=30,AB=50.点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于E.点M在线段AP上,点N在线段BP上,EM=EN,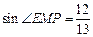 .
.
(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A、C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出函数的定义域;
(3)若△AME∽△ENB(△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应),求AP的长.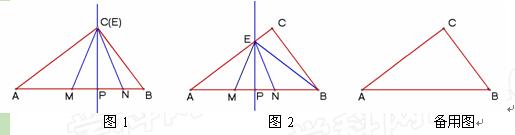 查看习题详情和答案>>
查看习题详情和答案>>
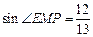 .
.(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A、C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出函数的定义域;
(3)若△AME∽△ENB(△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应),求AP的长.
 查看习题详情和答案>>
查看习题详情和答案>>
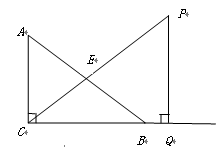
(本题满分14分)
如图,在 中,
中,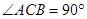 ,
, 是斜边
是斜边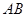 上的中线,
上的中线,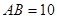 ,
,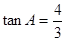 ,点
,点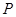 是
是 延长线上的一动点,过点
延长线上的一动点,过点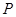 作
作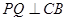 ,交
,交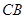 延长线于点
延长线于点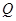 ,
,
设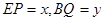 .
.
【小题1】(1)求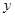 关于
关于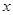 的函数关系式及定义域;(4分)
的函数关系式及定义域;(4分)
【小题2】(2)联结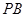 ,当
,当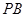 平分
平分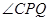 时,求
时,求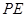 的长;(4分)
的长;(4分)
【小题3】(3)过点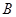 作
作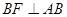 交
交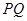 于
于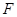 ,当
,当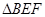 和
和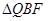 相似时,求
相似时,求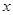
 的值.(6分)
的值.(6分)

 与x轴交于A、B两点,与y轴交于C点,点P从A
与x轴交于A、B两点,与y轴交于C点,点P从A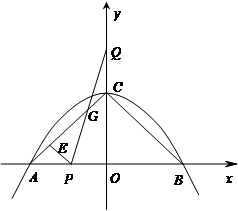 点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。