题目内容
(本题满分14分,其中第(1)题4分,第(2)题的第?、?小题分别为4分、6分)
如图1,在△ABC中,已知AB=15,cosB=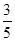 ,tanC=
,tanC=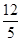 .点D为边BC上的动点(点D不与B、C重合),以D为圆心,BD为半径的⊙D交边AB于点E.
.点D为边BC上的动点(点D不与B、C重合),以D为圆心,BD为半径的⊙D交边AB于点E.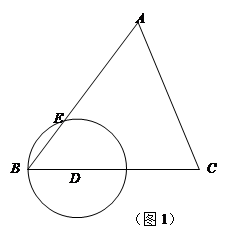
(1)设BD=x,AE=y,求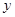 与
与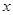 的函数关系式,并写出函数定域义;
的函数关系式,并写出函数定域义;
(2)如图2,点F为边AC上的动点,且满足BD=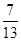 CF,联结DF.
CF,联结DF.
①当△ABC和△FDC相似时,求⊙D的半径;
② 当⊙D与以点F为圆心,FC为半径⊙F外切时,求⊙D的半径.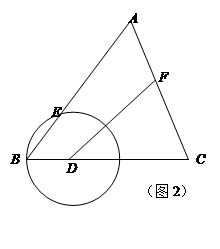
(1)y=-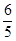 x+15 定义域0﹤x≦
x+15 定义域0﹤x≦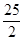 .(2)①⊙D的半径为
.(2)①⊙D的半径为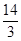 或
或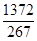 ,②⊙D的半径为
,②⊙D的半径为 。
。
解析试题分析:解:(1)过点D作DG⊥BE,垂足为E
∵DG过圆心,∴BE=2BG (1分)
在Rt△DGB中,cosB=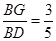 ,∵BD=x,∴BG=
,∵BD=x,∴BG= (1分)
(1分)
∴BE=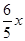 ,∵AB=15,∴y=15-
,∵AB=15,∴y=15-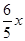 (1分)
(1分)
定义域为0<x≤ (1分)
(1分)
(2)①过点A作AH⊥BC,垂足为H
在Rt△ADH中,cosB=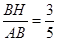
∵AB=15,∴BH=9,∴AH=12 (1分)
在Rt△AHC中,tanC=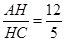
∴HC=5,∴BC=14 (1分)
设BD=x,则CF= ,DC=14-x
,DC=14-x
∵∠C=∠C,∴当△ABC和△FDC相似时,有
(ⅰ)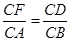 ,即
,即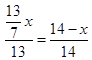 ,x=
,x=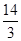 ,∴BD=
,∴BD=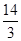 (1分)
(1分)
(ⅱ)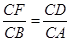 ,即
,即 ,x=
,x=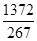 ,∴BD=
,∴BD=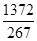 (1分)
(1分)
∴当△ABC和△FDC相似时,⊙D的半径为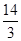 或
或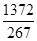
②过点F作FM⊥BC,垂足为M
在Rt△FMC中,tanC=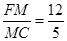 (1分)
(1分)
∴sinC= ,∵CF=
,∵CF= ,∴FM=
,∴FM=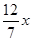 ,MC=
,MC=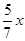 (1分)
(1分)
∴DM=14-x-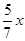 =14-
=14-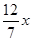 (1分)
(1分)
∴DF=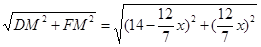 (1分)
(1分)
∵⊙D与⊙F外切,∴DF=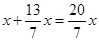 (1分)
(1分)
∴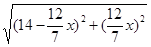 =
= ,解得x1=
,解得x1=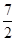 ,x2=
,x2= (舍去)
(舍去)
即BD=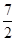 (1分)
(1分)
∴当⊙D与⊙F外切时,⊙D的半径为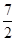 .
.
考点:一次函数的定义,相似三角形的定义及性质,切线定理,三角函数定义。
点评:本题综合性很强,涉及到的概念性质定理很多,计算又多,很容易出错,相关的知识点错综复杂,还有动点的问题,对学生的要求极高,要善于领会已知条件,及图像的变换过程,把握住已知条件,从基础入手,逐步的进行解答。题中说的定义域即是函数中自变量x的取值范围,本题属于难题,中考时一般以大题的形式出现。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 交
交

 (
( 且
且 ,
, 边经过点B时,求旋转角
边经过点B时,求旋转角 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥ 边于点E,联结BE.
边于点E,联结BE. 时,设
时,设 ,
, ,求
,求 与
与 之间的函数解析式及定义域;
之间的函数解析式及定义域; 时,求
时,求 的长.
的长. 

 满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分) (
( 且
且 ,
, 边经过点B时,求旋转角
边经过点B时,求旋转角 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥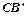 边于点E,联结BE.
边于点E,联结BE. 时,设
时,设 ,
,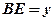 ,求
,求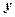 与
与 之间的函数解析式及定义域;
之间的函数解析式及定义域; 时,求
时,求 的长.
的长. 

 (
( 且
且 ,
, 边经过点B时,求旋转角
边经过点B时,求旋转角 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥ 边于点E,联结BE.
边于点E,联结BE.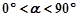 时,设
时,设 ,
, ,求
,求 与
与 之间的函数解析式及定义域;
之间的函数解析式及定义域; 时,求
时,求 的长.
的长. 
