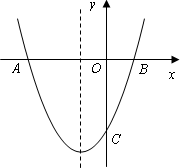
已知：抛物线y＝ax₂＋bx＋c经过A(1，0)、B(5，0)两点，最高点的纵坐标为4，与y轴交于点C．

(1)求该抛物线的解析式；

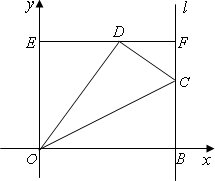
(2)若△ABC的外接圆⊙交y轴不同于点C的点D，⊙的弦DE平行于x轴，求直线CE的解析式；

已知：抛物线y＝ax²＋bx＋c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长(OB＜OC)是方程x²－10x＋16＝0的两个根，且抛物线的对称轴是直线x＝－2．

(1)求A、B、C三点的坐标；

(2)求此抛物线的表达式；

(3)求△ABC的面积；

(4)若点E是线段AB上的一个动点(与点A、点B不重合)，过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；

(5)在(4)的基础上试说明S是否存在最大值，若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．

已知：抛物线y＝ax²＋bx＋c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长(OB＜OC)是方程x²－10x＋16＝0的两个根，且抛物线的对称轴是直线x＝－2．

(1)求A、B、C三点的坐标；

(2)求此抛物线的表达式；

(3)求△ABC的面积；

(4)若点E是线段AB上的一个动点(与点A、点B不重合)，过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；

(5)在(4)的基础上试说明S是否存在最大值，若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．

已知：抛物线y＝ax²＋bx＋c(a≠0)的对称轴为x＝－1，与x轴交于A，B两点，与y轴交于点C，其中A(－3，0)、C(0，－2)．

(1)求这条抛物线的函数表达式．

(2)已知在对称轴上存在一点P，使得△PBC的周长最小．请求出点P的坐标．

(3)若点D是线段OC上的一个动点(不与点O、点C重合)．过点D作DE∥PC交x轴于点E．连接PD、PE．设CD的长为m，△PDE的面积为S．求S与m之间的函数关系式．试说明S是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．