摘要:直线的倾斜角与斜率:在平面直角坐标系中.对于一条与轴相交的直线.如果把轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为.那么就叫做直线的倾斜角. 当直线和轴平行或重合时.我们规定直线的倾斜角为0° 因此.根据定义.我们可以得到倾斜角的取值范围是0°≤<180° 倾斜角不是90°的直线.它的倾斜角的正切叫做这条直线的斜率.常用表示. 倾斜角是的直线没有斜率
网址:http://m.1010jiajiao.com/timu_id_4424099[举报]
在平面直角坐标系xOy中,如图,已知椭圆E:
+
=1(a>b>0)的左、右顶点分别为A1、A2,上、下顶点分别为B1、B2.设直线A1B1的倾斜角的正弦值为
,圆C与以线段OA2为直径的圆关于直线A1B1对称.
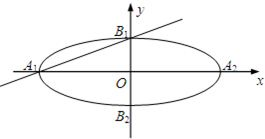
(1)求椭圆E的离心率;
(2)判断直线A1B1与圆C的位置关系,并说明理由;
(3)若圆C的面积为π,求圆C的方程. 查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |

(1)求椭圆E的离心率;
(2)判断直线A1B1与圆C的位置关系,并说明理由;
(3)若圆C的面积为π,求圆C的方程. 查看习题详情和答案>>
 在平面直角坐标系xoy中,椭圆C:
在平面直角坐标系xoy中,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C的标准方程;
(2)若θ=90°时,
| 1 |
| MF |
| 1 |
| NF |
5
| ||
| 9 |
(3)试问
| 1 |
| MF |
| 1 |
| NF |
在平面直角坐标系中,已知点A(1,0),点B在直线l:x=-1上运动,过点B与l垂直的直线和线段AB的垂直平分线相交于点M.
(1)求动点M的轨迹E的方程;
(2)过(1)中的轨迹E上的定点P(x0,y0)(y0>0)作两条直线分别与轨迹E相交于C(x1,y1),D(x2,y2)两点.试探究:当直线PC,PD的斜率存在且倾斜角互补时,直线CD的斜率是否为定值?若是,求出这个定值;若不是,说明理由. 查看习题详情和答案>>
(1)求动点M的轨迹E的方程;
(2)过(1)中的轨迹E上的定点P(x0,y0)(y0>0)作两条直线分别与轨迹E相交于C(x1,y1),D(x2,y2)两点.试探究:当直线PC,PD的斜率存在且倾斜角互补时,直线CD的斜率是否为定值?若是,求出这个定值;若不是,说明理由. 查看习题详情和答案>>
 中,如图,已知椭圆E:
中,如图,已知椭圆E: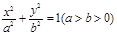 的左、右顶点分别为
的左、右顶点分别为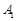 、
、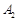 ,
,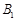 、
、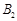 .设直线
.设直线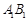 的倾斜角的正弦值为
的倾斜角的正弦值为 ,圆
,圆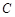 与以线段
与以线段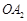 为直径的圆
为直径的圆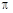 ,求圆
,求圆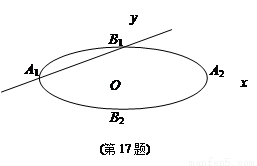
 中,如图,已知椭圆E:
中,如图,已知椭圆E: 的左、右顶点分别为
的左、右顶点分别为 、
、 ,上、下顶点分别为
,上、下顶点分别为 、
、 .设直线
.设直线 的倾斜角的正弦值为
的倾斜角的正弦值为 ,圆
,圆 与以线段
与以线段 为直径的圆关于直线
为直径的圆关于直线
 ,求圆
,求圆