摘要: (1) (2)解析:设F(x)=f(x)-2.即F(x)=alog2x+blog3x. 则F()=alog2+blog3=-(alog2x+blog3x)=-F(x). ∴F=-F()=-[f()-2]=-2. 即f-2=-2.故f=0 请在各题规定的黑色矩形区域内答题.超出该区域的答案无效! 17. A={x|-1<x≤5}. (1) 当m=3时.B={x|-1<x<3}. 则∁RB={x|x≤-1或x≥3}. ∴A∩(∁RB)={x|3≤x≤5}. (2)∵A={x|-1<x≤5}.A∩B={x|-1<x<4}. ∴有-42+2×4+m=0.解得m=8. 此时B={x|-2<x<4}.符合题意. 请在各题规定的黑色矩形区域内答题.超出该区域的答案无效 18. (1)证明:∵f(x+2)=-f(x). ∴f(x+4)=-f(x+2)=-[-f(x)]=f(x). ∴f(x)是以4为周期的周期函数. (2)当0≤x≤1时.f(x)=x. 设-1≤x≤0.则0≤-x≤1. ∴f(-x)=(-x)=-x.∵f(x)是奇函数. ∴f(-x)=-f(x).∴-f(x)=-x. 即f(x)=x.故f(x)=x(-1≤x≤1) 又设1<x<3.则-1<x-2<1. ∴f(x-2)=(x-2). 又∵f(x-2)=-f(2-x)=-f[(-x)+2] =-[-f(-x)]=-f(x). ∴-f(x)=(x-2). ∴f(x)=-(x-2)(1<x<3). ∴f(x)= 由f(x)=-.解得x=-1.∵f(x)是以4为周期的周期函数.故f(x)=-的所有x=4n-1(n∈Z).令0≤4n-1≤2010.则≤n≤502.又∵n∈Z.∴1≤n≤502(n∈Z).∴在[0,2010]上共有502个x使f(x)=-. 请在各题规定的黑色矩形区域内答题.超出该区域的答案无效 请在各题规定的黑色矩形区域内答题.超出该区域的答案无效! 19. (1)由已知得.函数的定义域为. 关于原点对称, 故是偶函数. (2)当时.在定义域内.函数与函数的单调性一致, . 易得.分别在区间内为单调递减. 所以.函数区间内为单调递减, (3)由已知得.由(2)可知.函数在内单调递减.所以有即 即 xsc解之得 请在各题规定的黑色矩形区域内答题.超出该区域的答案无效! 20. (1)当甲的用水量不超过6吨时.即时.乙的用水量也不会超过6吨.此时; 当甲的用水量超过6吨而乙的用水量没有超过6吨时.即时.此时 当甲乙的用水量都超过6吨时.即时. 此时 综上可知, (2)若 若 若 综上可知.甲的用水量为(吨) 付费(元) 乙的用水量为(吨) 付费(元) 答:略. 请在各题规定的黑色矩形区域内答题.超出该区域的答案无效! 21. (1) 法一:特殊点法 在直线上任取两点.--1分 则·即得点 -3 分 即得点 将和分别代入上得 则矩阵 则 法二:通法 设为直线上任意一点其在M的作用下变为 则 代入得: 其与完全一样得 则矩阵 则 消去参数.得直线的普通方程为-3分 .即. 两边同乘以得. 得⊙的直角坐标方程为 ---5分 (Ⅱ)圆心到直线的距离.所以直线和⊙相交-7分 (3).解:由.且. 得 --3分 又因为.则有2---5分 解不等式.得-------- 7分
网址:http://m.1010jiajiao.com/timu_id_4424089[举报]
(本小题13分)
有一批单放机原价为每台80元,两个商场均有销售,为了吸引顾客,两商场纷纷推出优惠政策。甲商场的优惠办法是:买一台减4元,买两台每台减8元,买三台每台减12元,......,依此类推,直到减到半价为止;乙商场的优惠办法是:一律7折。某单位欲为每位员工买一台单放机,问选择哪个商场购买比较划算?
查看习题详情和答案>>
(本小题13分)某饮料生产企业为了占有更多的市场份额,拟在2010年度进行
一系列促销活动,经过市场调查和测算,饮料的年销售量x万件与年促销费t万元间满足
 。已知2010年生产饮料的设备折旧,维修等固定费用为3 万元,每生产1万件
。已知2010年生产饮料的设备折旧,维修等固定费用为3 万元,每生产1万件
饮料需再投入32万元的生产费用,若将每件饮料的售价定为:其生产成本的150%与平均
每件促销费的一半之和,则该年生产的饮料正好能销售完。
(1)将2010年的利润y(万元)表示为促销费t(万元)的函数;
(2)该企业2010年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入—生产成本—促销费,生产成本=固定费用+生产费用)
查看习题详情和答案>>
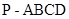 中,
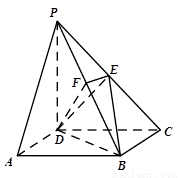
中,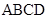 是矩形,侧棱PD⊥底面
是矩形,侧棱PD⊥底面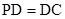 ,
,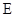 是
是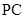 的中点,作
的中点,作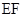 ⊥
⊥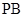 交
交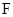 .
.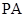 ∥平面
∥平面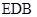 ;
;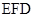 .
.
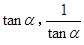 是关于
是关于 的方程
的方程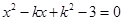 的两个实根,且
的两个实根,且 ,求
,求 的值
的值