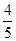摘要:例1.在的展开式中.奇数项的二项式系数的和等于偶数项的二项式系数的和 证明:在展开式中.令.则. 即. ∴. 即在的展开式中.奇数项的二项式系数的和等于偶数项的二项式系数的和. 说明:由性质(3)及例1知. 例2.已知.求: (1), (2), (3). 解:(1)当时..展开式右边为 ∴. 当时..∴. (2)令. ① 令. ② ①② 得:.∴ . (3)由展开式知:均为负.均为正. ∴由(2)中①+② 得:. ∴ . ∴ 例3.求2+-+(1+x)10展开式中x3的系数 解: =. ∴原式中实为这分子中的.则所求系数为 例4.在(x2+3x+2)5的展开式中.求x的系数 解:∵ ∴在(x+1)5展开式中.常数项为1.含x的项为. 在(2+x)5展开式中.常数项为25=32.含x的项为 ∴展开式中含x的项为 . ∴此展开式中x的系数为240 例5.已知的展开式中.第五项与第三项的二项式系数之比为14,3.求展开式的常数项 解:依题意 ∴3n/4!=4n(n-1)/2!n=10 设第r+1项为常数项.又 令. 此所求常数项为180
网址:http://m.1010jiajiao.com/timu_id_4421567[举报]
在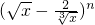 的展开式中,已知第5项的系数与第3项的系数之比是56:3.
的展开式中,已知第5项的系数与第3项的系数之比是56:3.
(1)求展开式中所有项的系数之和及奇数项的二项式系数之和;
(2)求展开式中的所有有理项;
(3)求展开式中系数绝对值最大的项.
注:所涉及的系数均用数字作答.
查看习题详情和答案>>
在![]() 的展开式中,已知第5项的系数与第3项的系数之比是56∶3.
的展开式中,已知第5项的系数与第3项的系数之比是56∶3.
(1)求展开式中所有项的系数之和及奇数项的二项式系数之和;
(2)求展开式中的所有有理项;
(3)求展开式中系数绝对值最大的项.
注:所涉及的系数均用数字作答
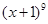 的二项展开式中任取
的二项展开式中任取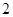 项,
项,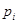 表示取出的
表示取出的 项系数为奇数的概率. 若用随机变量
项系数为奇数的概率. 若用随机变量 表示取出的
表示取出的 ( )
( )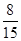 B.
B.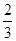 C.
C.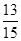 D.
D.