题目内容
在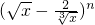 的展开式中,已知第5项的系数与第3项的系数之比是56:3.
的展开式中,已知第5项的系数与第3项的系数之比是56:3.
(1)求展开式中所有项的系数之和及奇数项的二项式系数之和;
(2)求展开式中的所有有理项;
(3)求展开式中系数绝对值最大的项.
注:所涉及的系数均用数字作答.
解:(1)由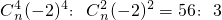 ,解得n=10…
,解得n=10…
所有项的系数之和为(1-2)10=1
奇数项的二项式系数之和为210-1=512
(2)因为通项:
当5-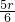 为整数,r可取0,6
为整数,r可取0,6
展开式是常数项,于是有理项为T1=x5和T7=13400
(3)设第r+1项系数绝对值最大,则
解得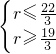 ,于是r只能为7
,于是r只能为7
所以系数绝对值最大的项为
分析:(1)利用第5项的系数与第3项的系数之比是56:3,求出n的值,即可通过x=1求展开式中所有项的系数之和及奇数项的二项式系数之和;
(2)通过二项式定理的通项公式,利用x的指数为0,求出展开式中的所有有理项;
(3)通过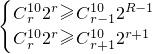 求展开式中系数绝对值最大的项.
求展开式中系数绝对值最大的项.
点评:本题是中档题,考查二项式定理系数的性质,通项公式的应用,考查计算能力.
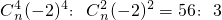 ,解得n=10…
,解得n=10…所有项的系数之和为(1-2)10=1
奇数项的二项式系数之和为210-1=512
(2)因为通项:

当5-
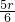 为整数,r可取0,6
为整数,r可取0,6展开式是常数项,于是有理项为T1=x5和T7=13400
(3)设第r+1项系数绝对值最大,则

解得
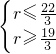 ,于是r只能为7
,于是r只能为7所以系数绝对值最大的项为

分析:(1)利用第5项的系数与第3项的系数之比是56:3,求出n的值,即可通过x=1求展开式中所有项的系数之和及奇数项的二项式系数之和;
(2)通过二项式定理的通项公式,利用x的指数为0,求出展开式中的所有有理项;
(3)通过
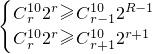 求展开式中系数绝对值最大的项.
求展开式中系数绝对值最大的项.点评:本题是中档题,考查二项式定理系数的性质,通项公式的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
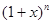 的展开式中,已知第三项与第五项的系数相等.
的展开式中,已知第三项与第五项的系数相等.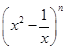 展开式中的系数最大的项和系数最小的项;
展开式中的系数最大的项和系数最小的项;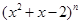 展开式中含
展开式中含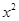 项的系数
项的系数