摘要：(一).三角形中的各种关系 设△ABC的三边为a.b.c.对应的三个角为A.B.C． 1．角与角关系:A+B+C = π. 2．边与边关系:a + b > c.b + c > a.c + a > b. a-b < c.b-c < a.c-a > b． 3．边与角关系: 1)正弦定理 2)余弦定理 c2 = a2+b2-2bccosC.b2 = a2+c2-2accosB.a2 = b2+c2-2bccosA． 它们的变形形式有:a = 2R sinA..． 3)射影定理: a＝b·cosC+c·cosB. b＝a·cosC+c·cosA. c＝a·cosB+c·cosA． 4)正切定理: -----. 5)模尔外得公式: 6)半角定理: 7)面积公式:
网址：http://m.1010jiajiao.com/timu_id_4420744[举报]
在古希腊，毕达哥拉斯学派把1，3，6，10，15，21，28，…，这些数叫做三角形数，其通项为
，前n项和为sn=
，如下图所示，有一列三角形数表，其位于三角形的三边及平行于某边的任一直线上的数（当数的个数不少于3时）都分别依次成等差数列，依次记各三角形数表中的所有数之和为an，则a1=
=
=2，a2=
=
=
．
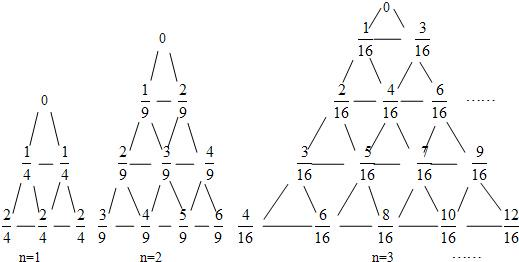
（1）求a3，a4，并写出an的表达式；
（2）令bn=
+
，证明2n＜b1+b2+b3+…+bn＜2n+2（n∈N*）．
查看习题详情和答案>>
| n(n+1) |
| 2 |
| n(n+1)(n+2) |
| 6 |
| 0+2+6 |
| 4 |
| 2(1+3) |
| 4 |
| 0+3+9+18 |
| 9 |
| 3(1+3+6) |
| 9 |
| 10 |
| 3 |
（1）求a3，a4，并写出an的表达式；
（2）令bn=
| an |
| an+1 |
| an+1 |
| an |
以下命题正确的是（ ）
（1）过一点一定存在和两条异面直线都平行的平面；
（2）两条平行线中的一条直线与一个平面平行，则另一条也必与这个平面平行；
（3）各面都是三角形的多面体是三棱锥；
（4）一条直线平行于一个平面，则夹在它们之间的平行线段长相等．
（1）过一点一定存在和两条异面直线都平行的平面；
（2）两条平行线中的一条直线与一个平面平行，则另一条也必与这个平面平行；
（3）各面都是三角形的多面体是三棱锥；
（4）一条直线平行于一个平面，则夹在它们之间的平行线段长相等．
| A、（1）（2）（3）（4） | B、（2）（3）（4） | C、（3）（4） | D、（4） |
把自然数按上小下大、左小右大的原则排成如图的三角形数表（每行比上一行多一个数）．设aij（i，j∈N*）是位于这个三角形数表中从上往下数第i行、从左往右数的第j个数（如a42=8）．（1）试用i表示aii（不要求证明）；
（2）若aij=2008，求i，j的值；
（3）记三角形数表从上往下数第n行的各数之和为bn，令cn=
|