题目内容
 把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数的第j个数(如a42=8).
把自然数按上小下大、左小右大的原则排成如图的三角形数表(每行比上一行多一个数).设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数的第j个数(如a42=8).(1)试用i表示aii(不要求证明);
(2)若aij=2008,求i,j的值;
(3)记三角形数表从上往下数第n行的各数之和为bn,令cn=
|
分析:(1)根据题意可知三角形数表中前n行的个数,进而可推知第i行的最后一个数进而可得aii.
(2)先求使得i是不等式
≥2008的最小正整数解.由
≥2008,得i2+i-4016≥0进而可解得i的范围确定i的最小值.
(3)先求得前n行的所有自然数的和进而根据bn=Sn-Sn-1求得bn,代入Cn中进而通过裂项法求得Tn.
(2)先求使得i是不等式
| i(i+1) |
| 2 |
| i(i+1) |
| 2 |
(3)先求得前n行的所有自然数的和进而根据bn=Sn-Sn-1求得bn,代入Cn中进而通过裂项法求得Tn.
解答:解:(1)∵三角形数表中前n行共有1+2++n=
个,
即第i行的最后一个数是
∴aii=
(2)由题意,先求使得i是不等式
≥2008的最小正整数解.
由
≥2008,得i2+i-4016≥0
∵i∈N*,∴i≥
>
=
=62.5,∴i=63
(3)前n行的所有自然数的和为Sn=
×
[
+1]=
则bn=Sn-Sn-1=
,
所以,当n≥2时,cn=
=
=
-
,Tn=1+(
-
)+(
-
)+(
-
)++(
-
)
=1+1+
-
-
=
-
-
=
-
当n=1时,Tn=1也适合,
∴Tn=
-
(n∈N*).
| n(n+1) |
| 2 |
即第i行的最后一个数是
| i(i+1) |
| 2 |
∴aii=
| i(i+1) |
| 2 |
(2)由题意,先求使得i是不等式
| i(i+1) |
| 2 |
由
| i(i+1) |
| 2 |
∵i∈N*,∴i≥
-1+
| ||
| 2 |
-1+
| ||
| 2 |
| -1+126 |
| 2 |
(3)前n行的所有自然数的和为Sn=
| 1 |
| 2 |
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
| n(n+1)(n2+n+2) |
| 2 |
则bn=Sn-Sn-1=
| n(n2+1) |
| 2 |
所以,当n≥2时,cn=
| n |
| bn-n |
| 2 |
| n2-1 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| n-1 |
| 1 |
| n+1 |
=1+1+
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
| 5 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
| 5 |
| 2 |
| 2n+1 |
| n(n+1) |
当n=1时,Tn=1也适合,
∴Tn=
| 5 |
| 2 |
| 2n+1 |
| n(n+1) |
点评:本题主要考查了数列的递推式.数列的递推式是高考中常考的题目,常与求数列的通项公式和前n项和一块考查,有时也涉及与函数、不等式等问题,综合性很强.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
1
|
表(每行比上一行多一个数):设![]() (i、j∈N*)是位于
(i、j∈N*)是位于
这个三角形数表中从上往下数第i行、从左往右数第j个
数,如![]() =8.若
=8.若![]() =2006,求i=_____;j=_____
=2006,求i=_____;j=_____
 ,若数列
,若数列
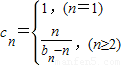 ,若数列{cn}的前n项和为Tn,求Tn.
,若数列{cn}的前n项和为Tn,求Tn.
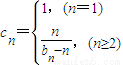 ,若数列{cn}的前n项和为Tn,求Tn.
,若数列{cn}的前n项和为Tn,求Tn.