摘要: 在解含有参数的不等式时.怎样进行讨论?(特别是指数和对数的底或)讨论完之后.要写出:综上所述.原不等式的解是--.
网址:http://m.1010jiajiao.com/timu_id_4420483[举报]
解关于 的不等式
的不等式

【解析】本试题主要考查了含有参数的二次不等式的求解,
首先对于二次项系数a的情况分为三种情况来讨论,
A=0,a>0,a<0,然后结合二次函数的根的情况和图像与x轴的位置关系,得到不等式的解集。
解:①若a=0,则原不等式变为-2x+2<0即x>1
此时原不等式解集为 ;
; 
②若a>0,则ⅰ) 时,原不等式的解集为
时,原不等式的解集为 ;
;
ⅱ) 时,原不等式的解集为
时,原不等式的解集为 ;
;
ⅲ) 时,原不等式的解集为
时,原不等式的解集为 。
。 
③若a<0,则原不等式变为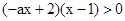
 原不等式的解集为
原不等式的解集为 。
。
查看习题详情和答案>>
(本小题满10分)注意:第(3)小题平行班学生不必做,特保班学生必须做。对于函数 ,若存在x0∈R,使
,若存在x0∈R,使 成立,则称x0为
成立,则称x0为 的不动点。已知函数
的不动点。已知函数 (a≠0)。
(a≠0)。
(1)当 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意实数b,函数 恒有两个相异的不动点,求a的取值范围;
恒有两个相异的不动点,求a的取值范围;
(3)(特保班做) 在(2)的条件下,若 图象上A、B两点的横坐标是函数
图象上A、B两点的横坐标是函数 的不动点,且A、B两点关于点
的不动点,且A、B两点关于点 对称,求
对称,求 的的最小值。
的的最小值。
查看习题详情和答案>>
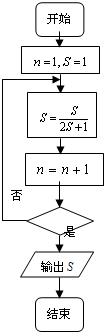 程序框图(即算法流程图)如图所示,其输出结果是
程序框图(即算法流程图)如图所示,其输出结果是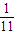 ,则判断框中所缺的条件是 . (用含有n的不等表示)
,则判断框中所缺的条件是 . (用含有n的不等表示)