摘要：15．已知三棱柱ABC-ABC.如图所示中底面边长和侧棱长均为a ,侧面AACC底面ABC.AB=. (1) 求异面直线AC与BC所成角的余弦值, (2) 求证:AB面ABC C B A 16．如图.点P为斜三棱柱ABC-ABC的侧棱BB上一点.PMBB交AA于点M,PNBB交CC于点N. M P A1 (1) B1 求证:CCMN (2) 在任意三角形DEF中有余弦定理DE.拓展到空间.类比三角形的余弦定理.写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角的关系式.并予以证明.
网址：http://m.1010jiajiao.com/timu_id_4420441[举报]
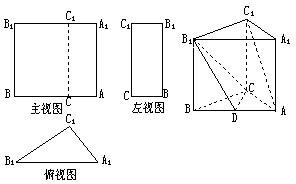已知三棱柱ABC-A1B1C1的三视图如图所示，其中主视图AA1B1B和左视图B1BCC1均为矩形，在俯视图△A1B1C1中，A1C1=3，A1B1=5，cos∠A1=| 3 | 5 |
（1）在三棱柱ABC-A1B1C1中，求证：BC⊥AC1；
（2）在三棱柱ABC-A1B1C1中，若D是底边AB的中点，求证：AC1∥平面CDB1．
（3）若三棱柱的高为5，求三视图中左视图的面积． 查看习题详情和答案>>
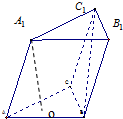已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2，A1在底面ABC内的射影O为底面△ABC的中心，如图所示：（1）联结BC1，若BC1=2
| 2 |
（2）联结A1C、A1B，求四棱锥A1-BCC1B1的体积．
已知三棱柱ABC-A1B1C1的底面为直角三角形，则棱与底面垂直，如图所示，D是棱CC1的中点，且∠ACB=90°，BC=1，AC=
，AA1=
（Ⅰ）证明：A1D⊥平面AB1C1；
（Ⅱ）求二面角B-AB1-C1的余弦值．
查看习题详情和答案>>
| 3 |
| 6 |
（Ⅰ）证明：A1D⊥平面AB1C1；
（Ⅱ）求二面角B-AB1-C1的余弦值．
的侧棱长和底面边长均为2，
在底面ABC内的射影O为底面△ABC的中心，如图所示：
，求异面直线
与
、
，求三棱锥C1－BCA1的体积．
的侧棱长和底面边长均为2，
在底面ABC内的射影O为底面△ABC的中心，如图所示：
，求异面直线
与
、
，求四棱锥
的体积．