题目内容
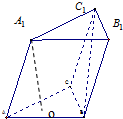 已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示:
已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示:(1)联结BC1,若BC1=2
| 2 |
(2)联结A1C、A1B,求四棱锥A1-BCC1B1的体积.
分析:(1)利用勾股定理证明BB1⊥B1C1,判断∠B1BC1为异面直线AA1与BC1所成的角,通过解三角形求得角;
(2)根据VA1-BCC1B1=2VA1-BB1C1=2VB-A1B1C1,只需利用三棱锥的换底性求得三棱锥三棱锥B-A1B1C1的体积,可得答案.
(2)根据VA1-BCC1B1=2VA1-BB1C1=2VB-A1B1C1,只需利用三棱锥的换底性求得三棱锥三棱锥B-A1B1C1的体积,可得答案.
解答:解:(1)∵三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,BC1=2
,
∴BB12+B1C12=BC12,∴BB1⊥B1C1,
∵AA1∥BB1,∴∠B1BC1为异面直线AA1与BC1所成的角,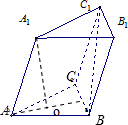
∠B1BC1=45°,∴异面直线AA1与BC1所成的角为45°;
(2)∵S△BCC1=S△BB1C1,
∴VA1-BCC1B1=2VA1-BB1C1=2VB-A1B1C1,
连接AO,∵A1在底面ABC内的射影O为底面△ABC的中心,
∴A1O为三棱锥B-A1B1C1的高,
∴OA=
×2×
=
,
∴四棱锥A1-BCC1B1的体积V=2×
×
×2×2×
×
=
.
| 2 |
∴BB12+B1C12=BC12,∴BB1⊥B1C1,
∵AA1∥BB1,∴∠B1BC1为异面直线AA1与BC1所成的角,

∠B1BC1=45°,∴异面直线AA1与BC1所成的角为45°;
(2)∵S△BCC1=S△BB1C1,
∴VA1-BCC1B1=2VA1-BB1C1=2VB-A1B1C1,
连接AO,∵A1在底面ABC内的射影O为底面△ABC的中心,
∴A1O为三棱锥B-A1B1C1的高,
∴OA=
| 2 |
| 3 |
| ||
| 2 |
2
| ||
| 3 |
∴四棱锥A1-BCC1B1的体积V=2×
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
2
| ||
| 3 |
| 4 |
| 3 |
点评:本题考查了异面直线所成的角及求法,考查了割补法求几何体的体积,割补法是求几何体体积的常用方法,必需熟练掌握.

练习册系列答案
相关题目
 如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则|
如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则|