摘要：例3． 若.求的取值范围. 错解 移项得.两边平方得 即 分析:忽略了满足不等式的在第一象限.上述解法引进了. 正解:即.由得 ∴
网址：http://m.1010jiajiao.com/timu_id_4420344[举报]
已知函数
满足：对于任意实数
，都有
恒成立，且当
时，
恒成立；
(1)求
的值，并例举满足题设条件的一个特殊的具体函数；
(2)判定函数
在R上的单调性，并加以证明；
(3)若函数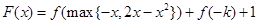
(其中
)有三个零点
,求
的取值范围.
查看习题详情和答案>>
已知函数f（x）（x∈R）满足：对于任意实数x，y，都有f(x+y)=f(x)+f(y)+
恒成立，且当x＞0时，f(x)＞-
恒成立；
（1）求f（0）的值，并例举满足题设条件的一个特殊的具体函数；
（2）判定函数f（x）在R上的单调性，并加以证明；
（3）若函数F（x）=f（max{-x，2x-x2}）+f（-k）+1（其中max{a，b}=
）有三个零点x1，x2，x3，求u=（x1+x2+x3）+x1•x2•x3的取值范围．
查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
（1）求f（0）的值，并例举满足题设条件的一个特殊的具体函数；
（2）判定函数f（x）在R上的单调性，并加以证明；
（3）若函数F（x）=f（max{-x，2x-x2}）+f（-k）+1（其中max{a，b}=
|
，
，当x＞0时，
，且对任意的a、b∈R，有f（a+b）=f（a）·f（b）.