摘要:已知椭圆的中心在原点.焦点在轴上.点.分别是椭圆的左.右焦点.在椭圆的右准线上的点.满足线段的中垂线过点.直线:为动直线.且直线与椭圆交于不同的两点.. (Ⅰ)求椭圆C的方程, (Ⅱ)若在椭圆上存在点.满足(为坐标原点). 求实数的取值范围, 的条件下.当取何值时.的面积最大.并求出这个最大值. 郑州市第四十七中学高中三年级第一次月考
网址:http://m.1010jiajiao.com/timu_id_4417380[举报]
(14分)已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且椭圆经过圆C:
,且椭圆经过圆C: ![]() 的圆心C。
的圆心C。
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ) 设![]() 是椭圆
是椭圆![]() 上的一点,过点
上的一点,过点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
已知椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,右准线的方程为
轴上,右准线的方程为![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,且
两点,且![]() 的中点坐标为
的中点坐标为![]() ,设
,设![]() 为椭圆
为椭圆![]() 的右顶点,
的右顶点,![]() 为椭圆
为椭圆![]() 上两点,且
上两点,且![]() ,
,![]() ,
,![]() 三者的平方成等差数列,则直线
三者的平方成等差数列,则直线![]() 和
和![]() 斜率之积的绝对值是否为定值,若是,请求出定值;若不是,请说明理由.
斜率之积的绝对值是否为定值,若是,请求出定值;若不是,请说明理由.
 的中心在原点,焦点在
的中心在原点,焦点在 轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为
轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为 的正方形(记为
的正方形(记为 )
) 是直线
是直线 与
与 与椭圆
与椭圆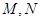 两点,当线段
两点,当线段 的中点落在正方形
的中点落在正方形