摘要:5.夹角公式:.
网址:http://m.1010jiajiao.com/timu_id_4416651[举报]
已知一列非零向量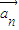 ,n∈N*,满足:
,n∈N*,满足: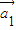 =(10,-5),
=(10,-5),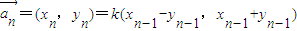 ,(n32 ).,其中k是非零常数.
,(n32 ).,其中k是非零常数.
(1)求数列{|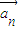 |}是的通项公式;
|}是的通项公式;
(2)求向量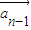 与
与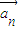 的夹角;(n≥2);
的夹角;(n≥2);
(3)当k= 时,把
时,把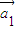 ,
,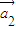 ,…,
,…,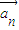 ,…中所有与
,…中所有与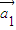 共线的向量按原来的顺序排成一列,记为
共线的向量按原来的顺序排成一列,记为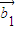 ,
,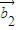 ,…,
,…,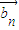 ,…,令
,…,令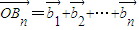 ,O为坐标原点,求点列{Bn}的极限点B的坐标.(注:若点坐标为(tn,sn),且
,O为坐标原点,求点列{Bn}的极限点B的坐标.(注:若点坐标为(tn,sn),且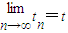 ,
,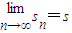 ,则称点B(t,s)为点列的极限点.)
,则称点B(t,s)为点列的极限点.)
查看习题详情和答案>>
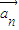 ,n∈N*,满足:
,n∈N*,满足: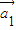 =(10,-5),
=(10,-5),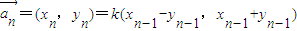 ,(n32 ).,其中k是非零常数.
,(n32 ).,其中k是非零常数.(1)求数列{|
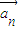 |}是的通项公式;
|}是的通项公式;(2)求向量
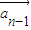 与
与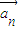 的夹角;(n≥2);
的夹角;(n≥2);(3)当k=
 时,把
时,把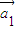 ,
,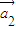 ,…,
,…,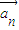 ,…中所有与
,…中所有与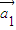 共线的向量按原来的顺序排成一列,记为
共线的向量按原来的顺序排成一列,记为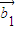 ,
,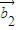 ,…,
,…,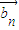 ,…,令
,…,令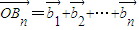 ,O为坐标原点,求点列{Bn}的极限点B的坐标.(注:若点坐标为(tn,sn),且
,O为坐标原点,求点列{Bn}的极限点B的坐标.(注:若点坐标为(tn,sn),且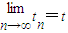 ,
,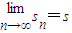 ,则称点B(t,s)为点列的极限点.)
,则称点B(t,s)为点列的极限点.)查看习题详情和答案>>
已知函数f(x)=px2+qx,其中p>0,p+q>1,对于数列{an},设它的前n项和为Sn,且满足Sn=f(n)(n∈N*).
(1)求数列{an}的通项公式,并证明an+1>an>1(n∈N*);
(2)求证:点M1(1,
),M2(2,
),M3(3,
),…,Mn(n,
)在同一直线l1上;
(3)若过点N1(1,a1),N2(2,a2)作直线l2,设l2与l1的夹角为θ,求tanθ的最大值.
查看习题详情和答案>>
(1)求数列{an}的通项公式,并证明an+1>an>1(n∈N*);
(2)求证:点M1(1,
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| Sn |
| n |
(3)若过点N1(1,a1),N2(2,a2)作直线l2,设l2与l1的夹角为θ,求tanθ的最大值.
已知函数f(x)=px2+qx,其中p>0,p+q>1,对于数列{an},设它的前n项和为Sn,且满足Sn=f(n)(n∈N*).
(1)求数列{an}的通项公式,并证明an+1>an>1(n∈N*);
(2)求证:点 在同一直线l1上;
在同一直线l1上;
(3)若过点N1(1,a1),N2(2,a2)作直线l2,设l2与l1的夹角为θ,求tanθ的最大值.
查看习题详情和答案>>
(1)求数列{an}的通项公式,并证明an+1>an>1(n∈N*);
(2)求证:点
 在同一直线l1上;
在同一直线l1上;(3)若过点N1(1,a1),N2(2,a2)作直线l2,设l2与l1的夹角为θ,求tanθ的最大值.
查看习题详情和答案>>