摘要：22．解:(Ⅰ)直角梯形ABCD的面积是 M底面. ∴ 四棱锥S-ABCD的体积是 M底面． (Ⅱ)延长BA.CD相交于点E.连结SE.则SE是所求二面角的棱． ∵ AD∥BC.BC = 2AD. ∴ EA = AB = SA.∴ SE⊥SB. ∵ SA⊥面ABCD.得面SEB⊥面EBC.EB是交线. 又BC⊥EB.∴ BC⊥面SEB.故SB是CS在面SEB上的射影.∴ CS⊥SE. 所以∠BSC是所求二面角的平面角． ∵ .BC =1.BC⊥SB. ∴ tg∠BSC ． 即所求二面角的正切值为．
网址：http://m.1010jiajiao.com/timu_id_4416389[举报]
本题（1）（2）（3）三个选答题，每小题5分，请考生任选1题作答，如果多做，则按所做的前1题计分．（1）（选修4-1，几何证明选讲）如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB=AD=a，CD=
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
（2）（选修4-4，坐标系与参数方程）在极坐标系（ρ，θ）（0≤θ≤2π）中，曲线ρ=2sinθ与ρcosθ=-1的交点的极坐标为
（
，
）
| 2 |
| 3π |
| 4 |
（
，
）
．| 2 |
| 3π |
| 4 |
（3）（选修4-1，不等式选讲）已知函数f（x）=|x-a|．若不等式f（x）≤3的解集为{x|-1≤x≤5}，则实数a的值为
a=2
a=2
．
本题（1）（2）（3）三个选答题，每小题5分，请考生任选1题作答，如果多做，则按所做的前1题计分．
（1）（选修4-1，几何证明选讲）如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB=AD=a，CD=
，点E，F分别为线段AB，CD的中点，则EF=________．
（2）（选修4-4，坐标系与参数方程）在极坐标系（ρ，θ）（0≤θ≤2π）中，曲线ρ=2sinθ与ρcosθ=-1的交点的极坐标为________．
（3）（选修4-1，不等式选讲）已知函数f（x）=|x-a|．若不等式f（x）≤3的解集为{x|-1≤x≤5}，则实数a的值为________．
查看习题详情和答案>>
本题（1）（2）（3）三个选答题，每小题5分，请考生任选1题作答，如果多做，则按所做的前1题计分．
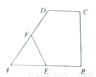
（1）（选修4-1，几何证明选讲）如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB=AD=a，CD=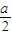
，点E，F分别为线段AB，CD的中点，则EF= ．
（2）（选修4-4，坐标系与参数方程）在极坐标系（ρ，θ）（0≤θ≤2π）中，曲线ρ=2sinθ与ρcosθ=-1的交点的极坐标为 ．
（3）（选修4-1，不等式选讲）已知函数f（x）=|x-a|．若不等式f（x）≤3的解集为{x|-1≤x≤5}，则实数a的值为 ．
查看习题详情和答案>>
（1）（选修4-1，几何证明选讲）如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB=AD=a，CD=
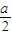，点E，F分别为线段AB，CD的中点，则EF= ．（2）（选修4-4，坐标系与参数方程）在极坐标系（ρ，θ）（0≤θ≤2π）中，曲线ρ=2sinθ与ρcosθ=-1的交点的极坐标为 ．
（3）（选修4-1，不等式选讲）已知函数f（x）=|x-a|．若不等式f（x）≤3的解集为{x|-1≤x≤5}，则实数a的值为 ．
查看习题详情和答案>>
| |||||||||||
，BM＝
，椭圆C以A，B为焦点且过点N
，问是否存在不平行AB的直线L与椭圆C交于P，Q两点，且|PE|＝|QE|，若存在，求出直线L与AB夹角的范围；若不存在，说明理由?
，BC＝
．椭圆C以A、B为焦点且经过点D．
，问是否存在不平行AB的直线l与椭圆C交于M、N两点且|ME|＝|NE|，若存在，求出直线l与AB夹角的范围，若不存在，说明理由．