题目内容
 本题(1)(2)(3)三个选答题,每小题5分,请考生任选1题作答,如果多做,则按所做的前1题计分.
本题(1)(2)(3)三个选答题,每小题5分,请考生任选1题作答,如果多做,则按所做的前1题计分.(1)(选修4-1,几何证明选讲)如图,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
(2)(选修4-4,坐标系与参数方程)在极坐标系(ρ,θ)(0≤θ≤2π)中,曲线ρ=2sinθ与ρcosθ=-1的交点的极坐标为
(
,
)
| 2 |
| 3π |
| 4 |
(
,
)
.| 2 |
| 3π |
| 4 |
(3)(选修4-1,不等式选讲)已知函数f(x)=|x-a|.若不等式f(x)≤3的解集为{x|-1≤x≤5},则实数a的值为
a=2
a=2
.分析:(1)要求EF的长,关键是关键是构造一个三角形,使EF位于该三角形,解三角形即可求解;
(2)先将原极坐标方程ρ=2sinθ与ρcosθ=-1化成直角坐标方程,再利用直角坐标方程求出交点,最后再转化成极坐标;
(3)根据绝对值不等式的解法,我们可得f(x)≤3的解集a-3≤x≤a+3,再由已知中f(x)≤3的解集为{x|-1≤x≤5},由此可以构造一个关于a的方程,解方程组,即可得到答案.
(2)先将原极坐标方程ρ=2sinθ与ρcosθ=-1化成直角坐标方程,再利用直角坐标方程求出交点,最后再转化成极坐标;
(3)根据绝对值不等式的解法,我们可得f(x)≤3的解集a-3≤x≤a+3,再由已知中f(x)≤3的解集为{x|-1≤x≤5},由此可以构造一个关于a的方程,解方程组,即可得到答案.
解答:解:(1)连接DE,
∵四边形ABCD为直角梯形,AB=AD=a,CD=
,CB⊥AB,点E,F分别为线段AB,AD的中点
∴△AED为直角三角形.则EF是RT△AED斜边上的中线,
由直角三角形斜边上的中线等于斜边的一半得,EF=
DE=
AB=
.
故答案为:
(2)两条曲线的普通方程分别为x2+y2=2y,x=-1.
解得
由
得点(-1,1),极坐标为 (
,
).
故答案为:(
,
).
(3)由|x-a|≤3得a-3≤x≤a+3,
所以
解之得a=2为所求,
故答案为:2.
∵四边形ABCD为直角梯形,AB=AD=a,CD=
| a |
| 2 |
∴△AED为直角三角形.则EF是RT△AED斜边上的中线,
由直角三角形斜边上的中线等于斜边的一半得,EF=
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
故答案为:
| a |
| 2 |
(2)两条曲线的普通方程分别为x2+y2=2y,x=-1.
解得
|
由
|
得点(-1,1),极坐标为 (
| 2 |
| 3π |
| 4 |
故答案为:(
| 2 |
| 3π |
| 4 |
(3)由|x-a|≤3得a-3≤x≤a+3,
所以
|
故答案为:2.
点评:(1)连接DE,构造含有线段EF的直角三角形是解答本题的关键,由此可得,解决平面几何的求值和证明问题,辅助线的添加是基础.
(2)本小题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.
(3)本题考查的知识点是带绝对值的函数、绝对值不等式的解法.
(2)本小题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.
(3)本题考查的知识点是带绝对值的函数、绝对值不等式的解法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,点E,F分别为线段AB,CD的中点,则EF= .
,点E,F分别为线段AB,CD的中点,则EF= .
 )
) 中,曲线
中,曲线 的交点的极坐标为
.
的交点的极坐标为
.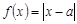 .若不等式
.若不等式 ,则实数
,则实数 的值为
.
的值为
. 本题(1)(2)(3)三个选答题,每小题5分,请考生任选1题作答,如果多做,则按所做的前1题计分.
本题(1)(2)(3)三个选答题,每小题5分,请考生任选1题作答,如果多做,则按所做的前1题计分. ,点E,F分别为线段AB,CD的中点,则EF=________.
,点E,F分别为线段AB,CD的中点,则EF=________.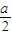 ,点E,F分别为线段AB,CD的中点,则EF= .
,点E,F分别为线段AB,CD的中点,则EF= .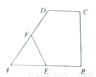
 CB⊥AB,AB=AD=
CB⊥AB,AB=AD= a,CD=
a,CD= ,点E,F分别为线段AB,CD的中点,则EF=" " .
,点E,F分别为线段AB,CD的中点,则EF=" " .
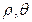 )
) 中,曲线
中,曲线 的交点的极坐标为 .
的交点的极坐标为 . .若不等式
.若不等式 ,则实数
,则实数 的值为 .
的值为 .