摘要：从5张100元.3张200元.2张300元的奥运预赛门票中任取3张.则所取3张中至少有2张价格相同的概率为( ) (A) (B) (C) (D)
网址：http://m.1010jiajiao.com/timu_id_4416348[举报]
某校高三数学理科组有10名教师，其中4名女老师；文科组有5位老师，其中3位女老师．现在采取分层抽样的方法（层内采用不放回简单随机抽样）从文、理两科中抽取3名教师进行“标、纲、题”测试．
（1）求从文、理两科各抽取的人数．
（2）求从理科组抽取的教师中恰有1名女教师的概率．
（3）记ξ表示抽取的3名教师中男教师人数，求ξ的概率分布列及数学期望．
查看习题详情和答案>>
（1）求从文、理两科各抽取的人数．
（2）求从理科组抽取的教师中恰有1名女教师的概率．
（3）记ξ表示抽取的3名教师中男教师人数，求ξ的概率分布列及数学期望．
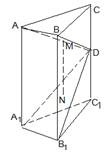
（文做理不做）已知：正四棱锥S-ABCD的高为| 3 |
（1）求证：EF∥平面SAD；
（2）试确定点M的位置，使得平面EFM⊥底面ABCD．
设h(x)=x+
，x∈[
，5]，其中m是不等于零的常数，
（1）（理）写出h（4x）的定义域；
（文）m=1时，直接写出h（x）的值域；
（2）（文、理）求h（x）的单调递增区间；
（3）已知函数f（x）（x∈[a，b]），定义：f1（x）=minf（t）|a≤t≤x（x∈[a，b]），f2（x）=maxf（t）|a≤t≤x（x∈[a，b]）．其中，minf（x）|x∈D表示函数f（x）在D上的最小值，maxf（x）|x∈D表示函数f（x）在D上的最大值．例如：f（x）=cosx，x∈[0，π]，则f1（x）=cosx，x∈[0，π]，f2（x）=1，x∈[0，π]．
（理）当m=1时，设M(x)=
+
，不等式t≤M1（x）-M2（x）≤n恒成立，求t，n的取值范围；
（文）当m=1时，|h1（x）-h2（x）|≤n恒成立，求n的取值范围． 查看习题详情和答案>>
| m |
| x |
| 1 |
| 4 |
（1）（理）写出h（4x）的定义域；
（文）m=1时，直接写出h（x）的值域；
（2）（文、理）求h（x）的单调递增区间；
（3）已知函数f（x）（x∈[a，b]），定义：f1（x）=minf（t）|a≤t≤x（x∈[a，b]），f2（x）=maxf（t）|a≤t≤x（x∈[a，b]）．其中，minf（x）|x∈D表示函数f（x）在D上的最小值，maxf（x）|x∈D表示函数f（x）在D上的最大值．例如：f（x）=cosx，x∈[0，π]，则f1（x）=cosx，x∈[0，π]，f2（x）=1，x∈[0，π]．
（理）当m=1时，设M(x)=
| h(x)+h(4x) |
| 2 |
| |h(x)-h(4x)| |
| 2 |
（文）当m=1时，|h1（x）-h2（x）|≤n恒成立，求n的取值范围． 查看习题详情和答案>>
中,
为棱
上的一动点,
,
分别为
,
的重心. 
；
在
的大小