摘要：圆与圆的位置关系 设两圆的半径分别为R和r.圆心距为d.则两圆的位置关系满足以下关系: 外离d>R+r 外切d＝R+r 相交R-r<d<R+r 内切d＝R-r 内含d<R-r
网址：http://m.1010jiajiao.com/timu_id_4415974[举报]
（本小题满分14分）
如图，椭圆
（
）的左、右焦点分别为F1（-1，0）、
F2（1，0），M、N是直线
上的两个动点，且
。
（1）设曲线C是以MN为直径的圆，试判断原点O与圆C的位置关系；
（2）若以MN为直径的圆中，最小圆的半径为2
，求椭圆的方程。
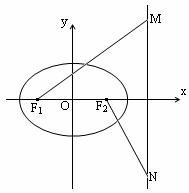
（本小题满分14分）
如图，椭圆
（
）的左、右焦点分别为F1（-1，0）、
F2（1，0），M、N是直线
上的两个动点，且
。
（1）设曲线C是以MN为直径的圆，试判断原点O与圆C的位置关系；
（2）若以MN为直径的圆中，最小圆的半径为2
，求椭圆的方程。
己知点F为抛物线C：y2=x的焦点，斜率为1的直线l交抛物线于不同两点P，Q．以F为圆心，以FP，FQ为半径作圆，分别交x轴负半轴于M，N，直线PM，QN交于点T．（I）判断直线PM与抛物线C的位置关系，并说明理由；
（II）连接FT，FQ，FP，记S1=S△PFT，S2=S△QFT，S3=S△PQT设直线l在y轴上的截距为m，当m何值时，
| S1S2 | S3 |
取得最小值，并求出取到最小值时直线l的方程．
取得最小值，并求出取到最小值时直线l的方程．