ÌâÄ¿ÄÚÈÝ
 ¼ºÖªµãFΪÅ×ÎïÏßC£ºy2=xµÄ½¹µã£¬Ð±ÂÊΪ1µÄÖ±Ïßl½»Å×ÎïÏßÓÚ²»Í¬Á½µãP£¬Q£®ÒÔFΪԲÐÄ£¬ÒÔFP£¬FQΪ°ë¾¶×÷Ô²£¬·Ö±ð½»xÖḺ°ëÖáÓÚM£¬N£¬Ö±ÏßPM£¬QN½»ÓÚµãT£®
¼ºÖªµãFΪÅ×ÎïÏßC£ºy2=xµÄ½¹µã£¬Ð±ÂÊΪ1µÄÖ±Ïßl½»Å×ÎïÏßÓÚ²»Í¬Á½µãP£¬Q£®ÒÔFΪԲÐÄ£¬ÒÔFP£¬FQΪ°ë¾¶×÷Ô²£¬·Ö±ð½»xÖḺ°ëÖáÓÚM£¬N£¬Ö±ÏßPM£¬QN½»ÓÚµãT£®£¨I£©ÅжÏÖ±ÏßPMÓëÅ×ÎïÏßCµÄλÖùØϵ£¬²¢ËµÃ÷ÀíÓÉ£»
£¨II£©Á¬½ÓFT£¬FQ£¬FP£¬¼ÇS1=S¡÷PFT£¬S2=S¡÷QFT£¬S3=S¡÷PQTÉèÖ±ÏßlÔÚyÖáÉϵĽؾàΪm£¬µ±mºÎֵʱ£¬
| S1S2 | S3 |
·ÖÎö£º£¨I£©Éè³öP£¬QµÄ×ø±ê£¬Çó³öÖ±ÏßPMµÄ·½³Ì£¬´úÈëÅ×ÎïÏß·½³Ì£¬ÀûÓÃÅбðʽ¿ÉµÃ½áÂÛ£»
£¨II£©½«Ö±ÏßPQ£ºy=x+m´úÈëy2=x¿ÉµÃy2-y+m=0£¬¼ÆËãµãFµ½Ö±ÏßPTµÄ¾àÀ룬µãQµ½Ö±ÏßPTµÄ¾àÀ룬´Ó¶ø¿ÉµÃ
=
=
=
£¬Í¬Àí
=
û¾¢¶ù¿ÉµÃ
=
£¬Áît=
£¾0£¬Ôò
=
(t3+
)=f(t)£¬ÀûÓõ¼Êý·¨£¬¼´¿ÉÇó³ö
µÄ×îСֵ£¬´Ó¶ø¿ÉµÃÈ¡µ½×îСֵʱֱÏßlµÄ·½³Ì£®
£¨II£©½«Ö±ÏßPQ£ºy=x+m´úÈëy2=x¿ÉµÃy2-y+m=0£¬¼ÆËãµãFµ½Ö±ÏßPTµÄ¾àÀ룬µãQµ½Ö±ÏßPTµÄ¾àÀ룬´Ó¶ø¿ÉµÃ
| S1 |
| S3 |
| d1 |
| d2 |
| 1+4y12 |
| 4(y1-y2)2 |
| 1+4y12 |
| 4(1-4m) |
| S2 |
| S3 |
| 1+4y22 |
| 4(1-4m) |
| S1S2 |
| S3 |
| 16m2-8m+5 | ||
64
|
| 1-4m |
| S1S2 |
| S3 |
| 1 |
| 64 |
| 4 |
| t |
| S1S2 |
| S3 |
½â´ð£º½â£º£¨I£©ÉèP£¨x1£¬y1£©£¬Q£¨x2£¬y2£©£¬ÓÉÌâÒâ¼°Å×ÎïÏߵĶ¨ÒåÖª£ºM£¨-x1£¬0£©£¬N£¨-x2£¬0£©£¬
¡àKMP=
=
¡àÖ±ÏßPM£ºy-y1=
(x-x1)£¬¼´x-2y1y+y12=0
´úÈëy2=x¿ÉµÃy2-2y1y+y12=0
¡ß¡÷=4y12-4y12=0
¡àÖ±ÏßPMÓëÅ×ÎïÏßCÏàÇУ»
£¨II£©Ö±ÏßPQ£ºy=x+m´úÈëy2=x¿ÉµÃy2-y+m=0
¡ày1+y2=1£¬y1y2=m
µãFµ½Ö±ÏßPTµÄ¾àÀëd1=
£»µãQµ½Ö±ÏßPTµÄ¾àÀëd2=
=
¡à
=
=
=
£¬Í¬Àí
=
ÓÖÖ±ÏßPMÓëQNµÄ½»µãT(y1y2£¬
)£¬¡àT(m£¬
)
¡àS3=
|PQ|d=
¡à
=
Áît=
£¾0£¬¡à
=
(t3+
)=f(t)
¡ßf¡ä(t)=
(3t2-
)=
¡àf£¨t£©ÔÚ(0£¬
)Éϵ¥µ÷µÝ¼õ£¬ÔÚ(
£¬+¡Þ)Éϵ¥µ÷µÝÔö
¡à
¡Ý
£¬´Ëʱm=
-
£¬¼´Ö±ÏßlµÄ·½³ÌΪy=x+
-
×ÛÉÏ¿ÉÖª£¬
µÄ×îСֵΪ
£¬È¡µ½×îСֵʱֱÏßlµÄ·½³ÌΪy=x+
-
£®
¡àKMP=
| y1 |
| 2x1 |
| 1 |
| 2y1 |
¡àÖ±ÏßPM£ºy-y1=
| 1 |
| 2y1 |
´úÈëy2=x¿ÉµÃy2-2y1y+y12=0
¡ß¡÷=4y12-4y12=0
¡àÖ±ÏßPMÓëÅ×ÎïÏßCÏàÇУ»
£¨II£©Ö±ÏßPQ£ºy=x+m´úÈëy2=x¿ÉµÃy2-y+m=0
¡ày1+y2=1£¬y1y2=m
µãFµ½Ö±ÏßPTµÄ¾àÀëd1=
|
| ||
|
| |x2-2y1y2+y12| | ||
|
| (y1-y2)2 | ||
|
¡à
| S1 |
| S3 |
| d1 |
| d2 |
| 1+4y12 |
| 4(y1-y2)2 |
| 1+4y12 |
| 4(1-4m) |
| S2 |
| S3 |
| 1+4y22 |
| 4(1-4m) |
ÓÖÖ±ÏßPMÓëQNµÄ½»µãT(y1y2£¬
| y1+y2 |
| 2 |
| 1 |
| 2 |
¡àS3=
| 1 |
| 2 |
| |y1-y2||1-4m| |
| 4 |
¡à
| S1S2 |
| S3 |
| 16m2-8m+5 | ||
64
|
Áît=
| 1-4m |
| S1S2 |
| S3 |
| 1 |
| 64 |
| 4 |
| t |
¡ßf¡ä(t)=
| 1 |
| 64 |
| 4 |
| t2 |
| 3t4-4 |
| 64t2 |
¡àf£¨t£©ÔÚ(0£¬
| 4 |
| ||
| 4 |
| ||
¡à
| S1S2 |
| S3 |
| 1 |
| 12 |
| 4 |
| ||
| 1 |
| 4 |
| ||
| 6 |
| 1 |
| 4 |
| ||
| 6 |
×ÛÉÏ¿ÉÖª£¬
| S1S2 |
| S3 |
| 1 |
| 12 |
| 4 |
| ||
| 1 |
| 4 |
| ||
| 6 |
µãÆÀ£º±¾Ì⿼²éÖ±ÏßÓëÅ×ÎïÏßµÄλÖùØϵ£¬¿¼²éÈý½ÇÐεÄÃæ»ý£¬¿¼²éµ¼Êý·¨Çóº¯ÊýµÄ×îÖµ£¬½âÌâµÄ¹Ø¼üÊǹ¹½¨º¯Êý¹Øϵʽ£¬ÊôÓÚÖеµÌ⣮

Á·Ï°²áϵÁдð°¸
 ÌôÕ½100µ¥Ôª¼ì²âÊÔ¾íϵÁдð°¸
ÌôÕ½100µ¥Ôª¼ì²âÊÔ¾íϵÁдð°¸
Ïà¹ØÌâÄ¿
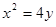 ÏàÇÐÓÚµãP£¨2£¬1£©£¬ÇÒÓëxÖá½»ÓÚµãA£¬¶¨µãB£¨2£¬0£©£®
ÏàÇÐÓÚµãP£¨2£¬1£©£¬ÇÒÓëxÖá½»ÓÚµãA£¬¶¨µãB£¨2£¬0£©£®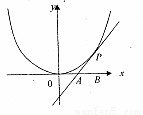
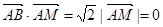 £¬ÇóµãM¹ì¼£CµÄ·½³Ì£º
£¬ÇóµãM¹ì¼£CµÄ·½³Ì£º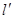 £¨Ð±Âʲ»ÎªÁ㣩Ó루1£©ÖеĹ켣C½»ÓÚ²»Í¬µÄÁ½µãE£¬F£¨EÔÚB¡¢FÖ®¼ä£©£¬ÊÔÇó¡÷OBEÓë¡÷OBFÃæ»ýÖ®±ÈµÄÈ¡Öµ·¶Î§£®
£¨Ð±Âʲ»ÎªÁ㣩Ó루1£©ÖеĹ켣C½»ÓÚ²»Í¬µÄÁ½µãE£¬F£¨EÔÚB¡¢FÖ®¼ä£©£¬ÊÔÇó¡÷OBEÓë¡÷OBFÃæ»ýÖ®±ÈµÄÈ¡Öµ·¶Î§£® È¡µÃ×îСֵ£¬²¢Çó³öÈ¡µ½×îСֵʱֱÏßlµÄ·½³Ì£®
È¡µÃ×îСֵ£¬²¢Çó³öÈ¡µ½×îСֵʱֱÏßlµÄ·½³Ì£®
 È¡µÃ×îСֵ£¬²¢Çó³öÈ¡µ½×îСֵʱֱÏßlµÄ·½³Ì£®
È¡µÃ×îСֵ£¬²¢Çó³öÈ¡µ½×îСֵʱֱÏßlµÄ·½³Ì£®