摘要:20.设函数(). (1)当时.的最小值为.求的值, (2)当时.设是函数图象上的两个动点.且在处的两切线互相平行.求证:直线必过定点.并求出此定点的坐标. 泰州市2008-2009学年度第二学期期末联考
网址:http://m.1010jiajiao.com/timu_id_4413140[举报]
(本题满分16分)
设函数f(x)=ax3-(a+b)x2+bx+c,其中a>0,b,c∈R.
(1)若![]() =0,求函数f(x)的单调增区间;
=0,求函数f(x)的单调增区间;
(2)求证:当0≤x≤1时,|![]() |≤
|≤![]() .(注:max{a,b}表示a,b中的最大值)
.(注:max{a,b}表示a,b中的最大值)
(本题满分16分)定义 ,
, ,…,
,…, 的“倒平均数”为
的“倒平均数”为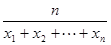 (
( ).已知数列
).已知数列 前
前 项的“倒平均数”为
项的“倒平均数”为 ,记
,记 (
( ).
).
(1)比较 与
与 的大小;
的大小;
(2)设函数 ,对(1)中的数列
,对(1)中的数列 ,是否存在实数
,是否存在实数 ,使得当
,使得当 时,
时, 对任意
对任意 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数 ;若不存在,说明理由.
;若不存在,说明理由.
(3)设数列 满足
满足 ,
, (
( 且
且 ),
), (
( 且
且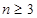 ),且
),且 是周期为
是周期为 的周期数列,设
的周期数列,设 为
为 前
前 项的“倒平均数”,求
项的“倒平均数”,求 .
.
查看习题详情和答案>>
(本题满分16分)
设函数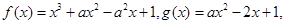 其中实数
其中实数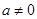 .
.
(1)当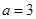 时,求函数
时,求函数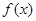 的单调区间;
的单调区间;
(2)当函数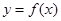 与
与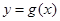 的图象只有一个公共点且
的图象只有一个公共点且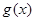 存在最小值时,
存在最小值时,
记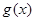 的最小值为
的最小值为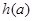 ,求函数
,求函数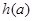 的值域;
的值域;
(3)若函数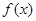 与
与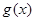 在区间
在区间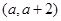 内均为增函数,求实数
内均为增函数,求实数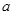 的取值范围.
的取值范围.
查看习题详情和答案>>