题目内容
(本题满分16分)定义 ,
, ,…,
,…, 的“倒平均数”为
的“倒平均数”为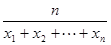 (
( ).已知数列
).已知数列 前
前 项的“倒平均数”为
项的“倒平均数”为 ,记
,记 (
( ).
).
(1)比较 与
与 的大小;
的大小;
(2)设函数 ,对(1)中的数列
,对(1)中的数列 ,是否存在实数
,是否存在实数 ,使得当
,使得当 时,
时, 对任意
对任意 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数 ;若不存在,说明理由.
;若不存在,说明理由.
(3)设数列 满足
满足 ,
, (
( 且
且 ),
), (
( 且
且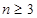 ),且
),且 是周期为
是周期为 的周期数列,设
的周期数列,设 为
为 前
前 项的“倒平均数”,求
项的“倒平均数”,求 .
.
【答案】
(1)设数列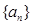 的前
的前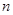 项和为
项和为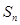 ,由题意得
,由题意得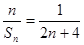 ,
,
所以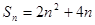 ,……(1分)
,……(1分)
当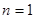 时,
时,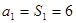 ,当
,当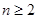 时,
时,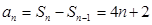 ,而
,而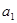 也满足此式.
也满足此式.
所以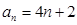 (
(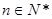 ).……(1分)
).……(1分)
所以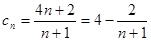 ,……(1分)
,……(1分)
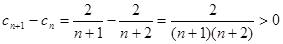 ,因此
,因此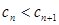 .……(1分)
.……(1分)
(2)假设存在实数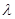 ,使得当
,使得当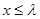 时,
时,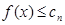 对任意
对任意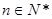 恒成立,
恒成立,
即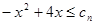 对任意
对任意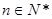 恒成立,……(2分)
恒成立,……(2分)
由(1)知数列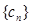 是递增数列,所以只要
是递增数列,所以只要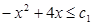 ,即
,即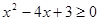 ,(2分)
,(2分)
解得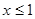 或
或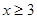 .……(1分)
.……(1分)
所以存在最大的实数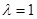 ,使得当
,使得当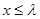 时,
时,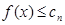 对任意
对任意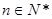 恒成立.…(1分)
恒成立.…(1分)
(3)由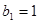 ,
,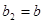 ,得
,得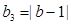 ,……(1分)
,……(1分)
① 若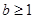 ,则
,则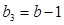 ,
,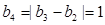 ,
,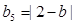 ,因为
,因为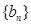 周期为
周期为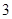 ,故
,故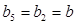 ,所以
,所以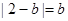 ,所以
,所以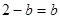 ,
,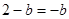 (舍),故
(舍),故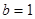 .
.
此时,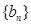 为
为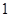 ,
,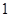 ,
, ,
,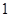 ,
,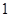 ,
, ,….符合题意.……(1分)
,….符合题意.……(1分)
② 若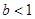 ,则
,则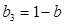 ,
,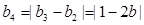 ,因为
,因为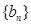 周期为
周期为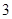 ,故
,故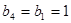 ,
,
所以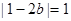 ,即
,即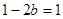 或
或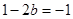 ,解得
,解得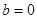 或
或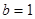 ,均不合题意.…(1分)
,均不合题意.…(1分)
设数列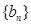 的前
的前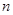 项和为
项和为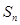 ,则对
,则对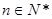 ,有
,有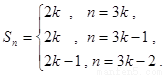 ……(1分)
……(1分)
即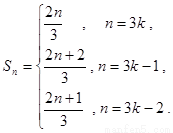 所以
所以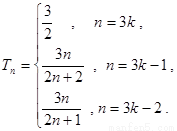 因此
因此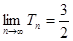 .(2分)
.(2分)
【解析】略

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 +
+ 的图象上的任意两点,且
的图象上的任意两点,且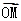 =
=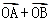 ),已知点M的横坐标为
),已知点M的横坐标为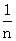 )+f(
)+f(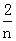 )+…+f(
)+…+f(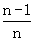 ),n∈N+且n≥2,求Sn;
),n∈N+且n≥2,求Sn;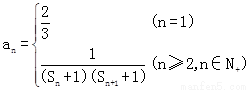 . Tn为其前n项的和,若Tn<
. Tn为其前n项的和,若Tn<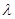 (Sn+1+1),对一切正整数都成立,求实数
(Sn+1+1),对一切正整数都成立,求实数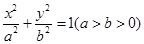 上有一个顶点到两个焦点之间的距离分别为
上有一个顶点到两个焦点之间的距离分别为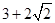 ,
,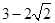 。
。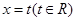 与椭圆相交于
与椭圆相交于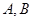 ,若
,若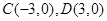 ,证明直线
,证明直线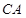 与直线
与直线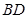 的交点
的交点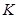 必在一条确定的双曲线上;
必在一条确定的双曲线上;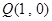 作直线
作直线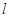 (与
(与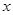 轴不垂直)与椭圆交于
轴不垂直)与椭圆交于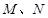 两点,与
两点,与 轴交于点
轴交于点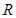 ,若
,若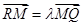 ,
,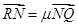 ,证明:
,证明: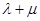 为定值。
为定值。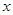 个,零件的实际出厂单价为P元,写出函数P=
个,零件的实际出厂单价为P元,写出函数P=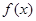 的表达式;
的表达式;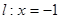 相切。
相切。  的直线与曲线M相交于A,B两点,A,B在直线
的直线与曲线M相交于A,B两点,A,B在直线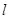 上的射影是
上的射影是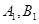 。求梯形
。求梯形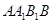 的面积;
的面积;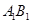 上的动点,当△ABC为直角三角形时,求点C的坐标。
上的动点,当△ABC为直角三角形时,求点C的坐标。 、
、 为坐标平面
为坐标平面 上的点,直线
上的点,直线 (
( 为坐标原点)与抛物线
为坐标原点)与抛物线 交于点
交于点 (异于
(异于 ,点
,点 上,试问当
上,试问当 为何值时,点
为何值时,点 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程 ;
; 在椭圆
在椭圆 上,试问:点
上,试问:点 、
、 是圆
是圆 ,试问:是否存在一个定圆
,试问:是否存在一个定圆 ,使直线
,使直线 恒与圆
恒与圆