摘要:1.如图所示是从大豆上收获的一个豆 荚.据此分析下列叙述正确的是( ) A.图示的豆荚是由一个子房发育而来的 B.形成图示的结果至少需要五粒花粉 C.该植物的子代个体发育的起点是图中的③ D.使用一定浓度的生长素可使②与③一样
网址:http://m.1010jiajiao.com/timu_id_4412126[举报]
如图所示是从一批产品中抽样得到的数据的频率分布直方图,由图形可以看出数据所落在范围的概率最大的是
A.(8.1,8.3) B.(8.2,8.4)
C.(8.4,8.5) D.(8.5,8.7)

杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律.如图所示是一个11阶杨辉三角:

(1)求第20行中从左到右的第4个数;
(2)若第n行中从左到右第14与第15个数的比为
,求n的值;
(3)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.试用含有m,k(m,k∈N*)的数学公式表示上述结论,并给予证明.
查看习题详情和答案>>

(1)求第20行中从左到右的第4个数;
(2)若第n行中从左到右第14与第15个数的比为
| 2 | 3 |
(3)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.试用含有m,k(m,k∈N*)的数学公式表示上述结论,并给予证明.
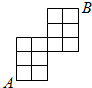 如图所示是某个区域的街道示意图(每个小矩形的边表示街道),则从A到B的最短线路有( )条.
如图所示是某个区域的街道示意图(每个小矩形的边表示街道),则从A到B的最短线路有( )条. 19、从某学校高三年级共800名男生中随机抽取50人测量身高.据测量被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…;第八组[190,195].如图所示是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
19、从某学校高三年级共800名男生中随机抽取50人测量身高.据测量被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…;第八组[190,195].如图所示是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.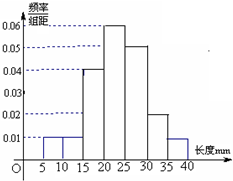 某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示.从抽样的100根棉花纤维中任意抽取一根,则其棉花纤维的长度小于20mm的概率为
某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示.从抽样的100根棉花纤维中任意抽取一根,则其棉花纤维的长度小于20mm的概率为