在△ABC中.sinA+cosA=.AC=2.AB=3.求tanA的值和△ABC的面积. 解法一:∵sinA+cosA=cos(A-45°)=. ∴cos(A-45°)=. 又0°＜A＜180°——青夏教育精英家教网—

摘要：在△ABC中.sinA+cosA=.AC=2.AB=3.求tanA的值和△ABC的面积. 解法一:∵sinA+cosA=cos(A-45°)=. ∴cos(A-45°)=. 又0°＜A＜180°. ∴A-45°=60°.A=105°. ∴tanA=tan==-2-. ∴sinA=sin105°=sin =sin45°cos60°+cos45°sin60°=. ∴S△ABC=AC·ABsinA =·2·3· =(+). 解法二:∵sinA+cosA=. ① ∴(sinA+cosA)2=.∴2sinAcosA=-. ∵0°＜A＜180°.∴sinA＞0.cosA＜0. ∴90°＜A＜180°. ∵(sinA-cosA)2=1-2sinAcosA=. ∴sinA-cosA=. ② ①+②得sinA=. ①-②得cosA=. ∴tanA==·=-2-.

网址：http://m.1010jiajiao.com/timu_id_4409191[举报]

【练】

（1）（2005高考北京卷）已知函数f(x)=－x³＋3x²＋9x＋a, （I）求f(x)的单调递减区间；（II）若f(x)在区间[－2，2]上的最大值为20，求它在该区间上的最小值．答案：（1）（－∞，－1），（3，＋∞）（2）－7

查看习题详情和答案>>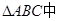

（2005•上海）在△ABC中，若∠C=90°，AC=BC=4，则

•

．

查看习题详情和答案>>

北京在，AB=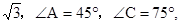则BC的长度是。