摘要：3．原本无色的物质在酶Ⅰ.酶Ⅱ和酶Ⅲ的催化作用下.转变为黑色素.即 无色物质→X物质→Y物质→黑色素 已知编码酶Ⅰ.酶Ⅱ和酶Ⅲ的基因分别为A.B.C.则基因型为AaBbCc的两个个体交配.出现黑色子代的概率为 A．1/64 B．3/64 C．27/64 D．9/64
网址：http://m.1010jiajiao.com/timu_id_4405251[举报]
俗话说“一石激起千层浪”，小时候在水上打“水漂”的游戏一定不会忘记吧．现在一个圆形波浪实验水池的中心已有两个振动源，在t秒内，它们引发的水面波动可分别由函数y1=sin t和y2=sin（t+
）来描述，当这两个振动源同时开始工作时，要使原本平静的水面保持平静，则需再增加一个振动源（假设不计其他因素，则水面波动由几个函数的和表达），请你写出这个新增振动源的函数解析式
．
查看习题详情和答案>>
| 2π | 3 |
在一个圆形波浪实验水池的中心有三个振动源，假如不计其它因素，在t秒内，它们引发的水面波动可分别由函数y1=sint，y2=sin(t+
)和y3=sin(t+
)描述．如果两个振动源同时启动，则水面波动由两个函数的和表达．在某一时刻使这三个振动源同时开始工作，那么，原本平静的水面将呈现怎样的状态，请说明理由．
查看习题详情和答案>>
| 2π |
| 3 |
| 4π |
| 3 |
某校课外兴趣小组的学生为了给学校边的一口被污染的池塘治污，他们通过实验后决定在池塘中投放一种能与水中的污染物质发生化学反应的药剂．已知每投放m（1≤m≤4，且m∈R）个单位的药剂，它在水中释放的浓度y（克/升）随着时间x（天）变化的函数关系式近似为y=m•f（x），其中f（x）=
若多次投放，则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和．根据经验，当水中药剂的浓度不低于4（克/升）时，它才能起到有效治污的作用．
（Ⅰ）若一次投放4个单位的药剂，则有效治污时间可达几天？
（Ⅱ）若第一次投放2个单位的药剂，6天后再投放m个单位的药剂，要使接下来的4天中能够持续有效治污，试求m的最小值．
查看习题详情和答案>>
|
（Ⅰ）若一次投放4个单位的药剂，则有效治污时间可达几天？
（Ⅱ）若第一次投放2个单位的药剂，6天后再投放m个单位的药剂，要使接下来的4天中能够持续有效治污，试求m的最小值．
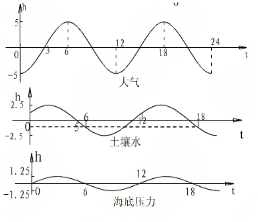大气、土壤水、海洋等物质在地球表面随着时间的变化而变化，这些物质对地壳压力负荷的变化会引起地壳的变形，在垂直方向尤为明显，根据上海某感测站的观测结果，该地的大气压力负荷、土壤水负荷、以及海底压力负荷引起的地壳垂向位移变化分别依次如图所示．