摘要:4.在应用与综合性题目中,当角不是特殊角,要“用反三角函数表示角 : (1) (2)arccosa表示[0.π]上余弦值等于a的角,a∈[-1,1]; (3) (4) 对于不是上述范围内的角,可借助诱导公式和三角函数线,找出与上述反三角的关系进而求出. 例如:sinα=0.3, α是钝角,则α=π-arcsin0.3.
网址:http://m.1010jiajiao.com/timu_id_4404501[举报]
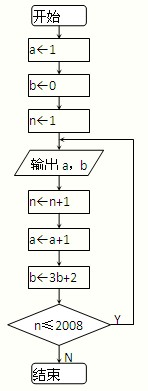 根据如图所示的流程图,将输出的a的值依次分别记为a1,a2,…,an,…,a2008,将输出的b的值依次分别记为b1,b2,…,bn,…,b2008.
根据如图所示的流程图,将输出的a的值依次分别记为a1,a2,…,an,…,a2008,将输出的b的值依次分别记为b1,b2,…,bn,…,b2008.(Ⅰ)求数列{an},{bn}通项公式;
(Ⅱ)依次在ak与ak+1中插入bk+1个3,就能得到一个新数列{cn},则a4是数列{cn}中的第几项?
(Ⅲ)设数列{cn}的前n项和为Sn,问是否存在这样的正整数m,使数列{cn}的前m项的和Sm=2008,如果存在,求出m的值,如果不存在,请说明理由.
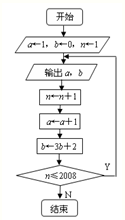 根据如图所示的程序框图,将输出a,b的值依次分别记为a1,a2,…,an,…,a2008;b1,b2,…,bn,…,b2008.
根据如图所示的程序框图,将输出a,b的值依次分别记为a1,a2,…,an,…,a2008;b1,b2,…,bn,…,b2008.(Ⅰ)求数列 { an} 的通项公式;
(Ⅱ)写出b1,b2,b3,b4,由此猜想{ bn}的通项公式,并证明你的证明;
(Ⅲ)在 ak与 ak+1中插入bk+1个3得到一个新数列 { cn },设数列 { cn }的前n项和为Sn,问是否存在这样的正整数m,使数列{ cn }的前m项的和Sm=2008,如果存在,求出m的值,如果不存在,请说明理由.
. 查看习题详情和答案>>
根据如图所示的程序框图,将输出a,b的值依次分别记为a1,a2,…,an,…,a2008;b1,b2,…,bn,…,b2008.
(Ⅰ)求数列 { an} 的通项公式;
(Ⅱ)写出b1,b2,b3,b4,由此猜想{ bn}的通项公式,并证明你的证明;
(Ⅲ)在 ak与 ak+1中插入bk+1个3得到一个新数列 { cn },设数列 { cn }的前n项和为Sn,问是否存在这样的正整数m,使数列{ cn }的前m项的和Sm=2008,如果存在,求出m的值,如果不存在,请说明理由.
.
查看习题详情和答案>>
(Ⅰ)求数列 { an} 的通项公式;
(Ⅱ)写出b1,b2,b3,b4,由此猜想{ bn}的通项公式,并证明你的证明;
(Ⅲ)在 ak与 ak+1中插入bk+1个3得到一个新数列 { cn },设数列 { cn }的前n项和为Sn,问是否存在这样的正整数m,使数列{ cn }的前m项的和Sm=2008,如果存在,求出m的值,如果不存在,请说明理由.
.

(2012•福州模拟)本题有(1)、(2)、(3)三个选做题,每题7分,请考生任选2题作答,满分l4分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填人括号中.
(1)选修4-2:矩阵与变换
利用矩阵解二元一次方程组
.
(2)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(cosθ+sinθ)=1.圆的参数方程为
(θ为参数,r>0),若直线l与圆C相切,求r的值.
(3)选修4-5:不等式选讲
已知a2+b2+c2=1(a,b,c∈R),求a+b+c的最大值.
查看习题详情和答案>>
(1)选修4-2:矩阵与变换
利用矩阵解二元一次方程组
|
(2)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(cosθ+sinθ)=1.圆的参数方程为
|
(3)选修4-5:不等式选讲
已知a2+b2+c2=1(a,b,c∈R),求a+b+c的最大值.
本题有(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)选修4-2:矩阵与变换
已知矩阵M=
,向量
=
.
(I)求矩阵M的特征值λ1、λ2和特征向量
1和
;
(II)求M6
的值.
(2)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线C的参数方程为
(α为参数).以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ-
)=2
.
(Ⅰ)求直线l的直角坐标方程;
(Ⅱ)点P为曲线C上的动点,求点P到直线l距离的最大值.
(3)选修4-5:不等式选讲
(Ⅰ)已知:a、b、c∈R+,求证:a2+b2+c2≥
(a+b+c)2;
(Ⅱ)某长方体从一个顶点出发的三条棱长之和等于3,求其对角线长的最小值.
查看习题详情和答案>>
(1)选修4-2:矩阵与变换
已知矩阵M=
|
| ξ |
|
(I)求矩阵M的特征值λ1、λ2和特征向量
| ξ |
| ξ2 |
(II)求M6
| ξ |
(2)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线C的参数方程为
|
| π |
| 4 |
| 2 |
(Ⅰ)求直线l的直角坐标方程;
(Ⅱ)点P为曲线C上的动点,求点P到直线l距离的最大值.
(3)选修4-5:不等式选讲
(Ⅰ)已知:a、b、c∈R+,求证:a2+b2+c2≥
| 1 |
| 3 |
(Ⅱ)某长方体从一个顶点出发的三条棱长之和等于3,求其对角线长的最小值.