题目内容
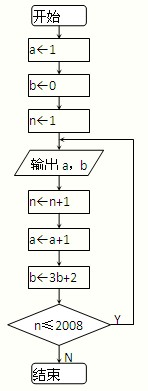 根据如图所示的流程图,将输出的a的值依次分别记为a1,a2,…,an,…,a2008,将输出的b的值依次分别记为b1,b2,…,bn,…,b2008.
根据如图所示的流程图,将输出的a的值依次分别记为a1,a2,…,an,…,a2008,将输出的b的值依次分别记为b1,b2,…,bn,…,b2008.(Ⅰ)求数列{an},{bn}通项公式;
(Ⅱ)依次在ak与ak+1中插入bk+1个3,就能得到一个新数列{cn},则a4是数列{cn}中的第几项?
(Ⅲ)设数列{cn}的前n项和为Sn,问是否存在这样的正整数m,使数列{cn}的前m项的和Sm=2008,如果存在,求出m的值,如果不存在,请说明理由.
分析:(I)由已知中的程序流程图,可得a1=1,an+1=an+1,根据等差数列的定义,可得数列{an}是公差为1,首项为1的等差数列,进而可得出数列{an}的通项公式,进而根据b1=0,bn+1=3bn+2,得到{bn+1}是首项为1,公比为3的等比数列,先求出数列{bn+1}的通项公式,进而得到数列{bn}的通项公式.
(II)由已知中数列{cn}的构造法则,我们由a4=4,我们列举出数列{cn}中4之间的所有项,即可得到结论;
(III)由(II)中数列{cn}的构造法则,及(I)中结论,我们可得ak项(含ak)前的所有项的和是:(1+2+…k)+(31+32+…+3k)=
+
,易分析出k=7时,Sm<2008,k=8时,Sm>2008,结合2008-1120为3的倍数,故存在m的值满足条件,进而可得到结果.
(II)由已知中数列{cn}的构造法则,我们由a4=4,我们列举出数列{cn}中4之间的所有项,即可得到结论;
(III)由(II)中数列{cn}的构造法则,及(I)中结论,我们可得ak项(含ak)前的所有项的和是:(1+2+…k)+(31+32+…+3k)=
| k(k+1) |
| 2 |
| 3k-3 |
| 2 |
解答:解:(Ⅰ)由流程图,a1=1,an+1=an+1,
∴{an}是公差为1的等差数列.∴an=n.(2分)
由流程图,b1=0,bn+1=3bn+2,
∴bn+1+1=3(bn+1).
∴{bn+1}是首项为1,公比为3的等比数列.
∴bn+1=(b1+1)×3n-1=3n-1,∴bn=3n-1-1.(6分)
(Ⅱ){cn}的前几项为1,
, 2,
3,
, 4, …,a4=4,∴a4是数列{cn}中的第17项.(9分)
(Ⅲ)数列{cn}中,ak项(含ak)前的所有项的和是:(1+2+…k)+(31+32+…+3k)=
+
,(11分)
当k=7时,其和为28+
=1120<2008,
当k=8时,其和为36+
=3315>2008.(13分)
又因为2008-1120=888=296×3,是3的倍数,
故当m=7+(1+3+32+…35)+296=667时,Sm=2008.(16分)
∴{an}是公差为1的等差数列.∴an=n.(2分)
由流程图,b1=0,bn+1=3bn+2,
∴bn+1+1=3(bn+1).
∴{bn+1}是首项为1,公比为3的等比数列.
∴bn+1=(b1+1)×3n-1=3n-1,∴bn=3n-1-1.(6分)
(Ⅱ){cn}的前几项为1,
| ||
| 1个3 |
| ||
| 3个3 |
| ||
| 9个3 |
(Ⅲ)数列{cn}中,ak项(含ak)前的所有项的和是:(1+2+…k)+(31+32+…+3k)=
| k(k+1) |
| 2 |
| 3k-3 |
| 2 |
当k=7时,其和为28+
| 37-3 |
| 2 |
当k=8时,其和为36+
| 38-3 |
| 2 |
又因为2008-1120=888=296×3,是3的倍数,
故当m=7+(1+3+32+…35)+296=667时,Sm=2008.(16分)
点评:本题考查的知识点是程序框图,等差数列的通项公式,等比数列的通项公式,数列求和,是数列问题比较综合的考查,难度比较大,其中根据已知中的程序框图,分析出数列{an},{bn}各项之间的关系,进而求出{an},{bn}的通项公式,是解答本题的关键.

练习册系列答案
相关题目
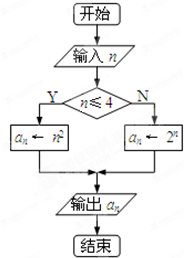 根据如图所示的流程图,当输入的正整数n的值为5时,输出的an的值是
根据如图所示的流程图,当输入的正整数n的值为5时,输出的an的值是
 (2012•盐城三模)根据如图所示的流程图,若输入x的值为-7.5,则输出y的值为
(2012•盐城三模)根据如图所示的流程图,若输入x的值为-7.5,则输出y的值为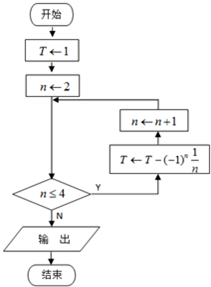 (2013•镇江二模)根据如图所示的流程图,输出的结果T为
(2013•镇江二模)根据如图所示的流程图,输出的结果T为