摘要:例1.(1)求的展开式的第四项的系数, (2)求的展开式中的系数及二项式系数 解:的展开式的第四项是. ∴的展开式的第四项的系数是. (2)∵的展开式的通项是. ∴.. ∴的系数.的二项式系数. 例2.求的展开式中的系数 分析:要把上式展开.必须先把三项中的某两项结合起来.看成一项.才可以用二项式定理展开.然后再用一次二项式定理..也可以先把三项式分解成两个二项式的积.再用二项式定理展开 解: . 显然.上式中只有第四项中含的项. ∴展开式中含的项的系数是 : ∴展开式中含的项的系数是. 例3.已知 的展开式中含项的系数为.求展开式中含项的系数最小值 分析:展开式中含项的系数是关于的关系式.由展开式中含项的系数为.可得.从而转化为关于或的二次函数求解 解:展开式中含的项为 ∴.即. 展开式中含的项的系数为 . ∵. ∴. ∴ .∴当时.取最小值.但. ∴ 时.即项的系数最小.最小值为.此时. 例4.已知的展开式中.前三项系数的绝对值依次成等差数列. (1)证明展开式中没有常数项,(2)求展开式中所有的有理项 解:由题意:.即.∴舍去) ∴ ①若是常数项.则.即. ∵.这不可能.∴展开式中没有常数项, ②若是有理项.当且仅当为整数. ∴.∴ . 即 展开式中有三项有理项.分别是:..
网址:http://m.1010jiajiao.com/timu_id_4400748[举报]
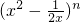 (n∈N*)的展开式中第四项的系数与第二项的系数的比是7:3.
(n∈N*)的展开式中第四项的系数与第二项的系数的比是7:3. (n∈N*)的展开式中第四项的系数与第二项的系数的比是7:3.
(n∈N*)的展开式中第四项的系数与第二项的系数的比是7:3.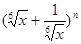 展开式中第二、三、四项的二项式系数成等差数列.
展开式中第二、三、四项的二项式系数成等差数列.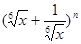 展开式中第二、三、四项的二项式系数成等差数列.
展开式中第二、三、四项的二项式系数成等差数列.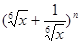 展开式中第二、三、四项的二项式系数成等差数列.
展开式中第二、三、四项的二项式系数成等差数列.