网址:http://m.1010jiajiao.com/timu_id_439781[举报]
一、选择题:本大题共10小题,每小题5分,共50分。
1.C 2.D 3.A 4.C 5.A 6.D 7.D 8.B 9.C 10.B
二、填空题:本答题共6小题,每小题4分,共24分。
11. = 22 12.
= 22 12. 13.594 14.m=
13.594 14.m=
15. 16.1,3
16.1,3
三、解答题:本大题共6小题,共76分。
17.(本小题满分12分)
解:(1)将函数 (ω>0)的图象按向量
(ω>0)的图象按向量 平移,平移后的图象所对应的解析式为
平移,平移后的图象所对应的解析式为 ,由图象知,
,由图象知, ,所以
,所以 .
.
∴所求解析式为 (6分)
(6分)
(2)∵sin(2α+ )=sin2α?cos
)=sin2α?cos +cos2αsin
+cos2αsin =sinαcosα+
=sinαcosα+ (cos2α-sin2α)
(cos2α-sin2α)
= =
= (10分)
(10分)
将tanα= 代入得
代入得
sin(2α+ )=
)= =
= (12分)
(12分)
另解:由tanα= 得:cosα=
得:cosα= ,sinα=
,sinα= 。?
(10分)
。?
(10分)
∴sin(2α+ )=sin2α?cos
)=sin2α?cos +cos2α?sin
+cos2α?sin =sinαcosα+
=sinαcosα+ (2cos2α-1)=
(2cos2α-1)=  =
= (12分)
(12分)
18.(本小题满分12分)
解:设开关JA,JB ,JC ,JD 能够闭合的事件依次为A、B、C、D,则P(A)=P(D)=0.7,P(B)=P(C)=0.8
(1)P(B?C)=P(B)? P(c)=0.8×0.8=0.64 (6分)
(2)JA不能工作的概率为
JD不能工作的概率为 (8分)
(8分)
 (10分)
(10分)

所以整条线路能正常工作的概率为0.9676 (12分)
答:9月份这段线路能正常工作的概率为0.9676。 (14分)
 19.(本小题满分12分)
19.(本小题满分12分)
解:(1)∵CF⊥平面ABC,∴AC是AF在平面ABC的射影
∵△ABC为边长是 的等边三角形,M为AC中点
的等边三角形,M为AC中点
∴BM⊥AC,
∴AF⊥BM (3分)
(2)延长FE、CB交于一点N,则AN是平面AEF与平面ABC的交线
∵BE⊥平面ABC, CF⊥平面ABC
∴BE∥CF,∵CF=AB = 2BE,∴BE是△FCN的中位线B是CN的中点,
∴AN∥BM, AN⊥AC
∴AN⊥FA,∴∠FAC为所求二面角的平面角 (6分)
∵CF=AC, ∴∠FAC=45° (7分)
(3)V=VF-CAN-VE-ABN (9分)
=

 ×a-
×a-
 2a×a×sin1200×
2a×a×sin1200× (11分)
(11分)
= -
- =
= (12分)
(12分)
注:第(2)问利用 指明S/,S也可;第(3)问可用分割的方法,相应给分。
指明S/,S也可;第(3)问可用分割的方法,相应给分。
20.(本小题满分12分)
解(1)∵f′(x)=-x2+4ax-3a2=-(x-3a)(x-a),由f′(x)>0得:a<x<3a
由f′(x)<0得,x<a或x>3a,
则函数f(x)的单调递增区间为(a,3a),单调递减区间为(-∞,a)和(3a,+∞)列表如下:
X
(-∞,a)
a
(a, 3a)
3a
(3a,+ ∞)
f′(x)
―
0
+
0
―
f(x)
ㄋ
- a3+b
a3+b
ㄊ
b
ㄋ
∴函数f(x)的极大值为b,极小值为- a3+b (6分)
a3+b (6分)
(2)
 上单调递减,
上单调递减,
因此
∵不等式|f′(x)|≤a恒成立,
即a的取值范围是 (12分)
(12分)
21.(本小题满分14分)
(1)由 ,得
,得 ,
, (2分)
(2分)

 ,
(4分)
,
(4分)
又 成等差数列,
成等差数列,
 (5分)
(5分)
即:
即: ,解之得:
,解之得: 或
或 , (6分)
, (6分)
经检验, 是增根,∴
是增根,∴ .
(7分)
.
(7分)
(2)证明:


 (9分)
(9分)

 时等号成立 (10分)
时等号成立 (10分)
此时
即: 。 (14分)
。 (14分)
22.(本小题满分14分)
解(1)由双曲线C: 知F(2,0), 第一、三象限的渐近线
知F(2,0), 第一、三象限的渐近线 :
:
设点P ,∵FP⊥
,∵FP⊥ ,∴
,∴ ,∴x=
,∴x= ,∴P
,∴P , A
, A
 ,
,
 ,∴
,∴ =
=
(2)由 得:
得: ,
,
设 ,
, ,M、N的中点为H
,M、N的中点为H
则 ,
,
 ,
, ,
, ,
,
即H ,
,
则线段MN的垂直平分线为: ,
,
将点B(0,-1),的坐标代入,化简得: ,
,
则由 得:
得: ,解之得
,解之得 或
或 ,
,
又 ,所以
,所以 ,
,
故m的取值范围是 。
。
C.选修4-4:坐标系与参数方程
在极坐标系下,已知圆O: 和直线
和直线 ,
,
(1)求圆O和直线 的直角坐标方程;(2)当
的直角坐标方程;(2)当 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
D.选修4-5:不等式证明选讲
对于任意实数
 和
和 ,不等式
,不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
在极坐标系下,已知圆O:
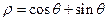 和直线
和直线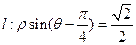 ,
,(1)求圆O和直线
 的直角坐标方程;(2)当
的直角坐标方程;(2)当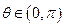 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.D.选修4-5:不等式证明选讲
对于任意实数
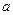
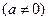 和
和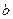 ,不等式
,不等式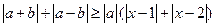 恒成立,试求实数
恒成立,试求实数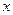 的取值范围.
的取值范围.









 作圆
作圆 的弦,其中弦长为整数的共有 ( )
的弦,其中弦长为整数的共有 ( )