摘要：①式减②式得..变形得.
网址：http://m.1010jiajiao.com/timu_id_43578[举报]
设函数f（x）=Asin（ωx+φ）A＞0，ω＞0，|φ|＜
）的最高点D的坐标为（
，2），由最高点D运动到相邻最低点时，函数图形与x的交点的坐标为（
，0）；
（1）求函数f（x）的解析式．
（2）当x∈[-
，
]时，求函数f（x）的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值．
（3）将函数y=f（x）的图象向右平移
个单位，得到函数y=g（x）的图象，求函数y=g（x）的单调减区间．
查看习题详情和答案>>
| π |
| 2 |
| π |
| 8 |
| 3π |
| 8 |
（1）求函数f（x）的解析式．
（2）当x∈[-
| π |
| 4 |
| π |
| 4 |
（3）将函数y=f（x）的图象向右平移
| π |
| 4 |
设函数f（x）=Asin（ωx+φ）A＞0，ω＞0，|φ|＜
）的最高点D的坐标为（
，2），由最高点D运动到相邻最低点时，函数图形与x的交点的坐标为（
，0）；
（1）求函数f（x）的解析式．
（2）当x∈[-
，
]时，求函数f（x）的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值．
（3）将函数y=f（x）的图象向右平移
个单位，得到函数y=g（x）的图象，求函数y=g（x）的单调减区间．
查看习题详情和答案>>
| π |
| 2 |
| π |
| 8 |
| 3π |
| 8 |
（1）求函数f（x）的解析式．
（2）当x∈[-
| π |
| 4 |
| π |
| 4 |
（3）将函数y=f（x）的图象向右平移
| π |
| 4 |
设函数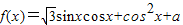
．
（Ⅰ）写出函数的最小正周期及单调递减区间；
（Ⅱ）当x∈[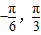
]时，函数f（x）的最大值与最小值的和为
，求f（x）的解析式；
（Ⅲ）将满足（Ⅱ）的函数f（x）的图象向右平移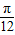
个单位，纵坐标不变横坐标变为原来的2倍，再向下平移
，得到函数g（x），求g（x）图象与x轴的正半轴、直线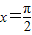
所围成图形的面积．
查看习题详情和答案>>
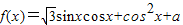．（Ⅰ）写出函数的最小正周期及单调递减区间；
（Ⅱ）当x∈[
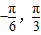]时，函数f（x）的最大值与最小值的和为，求f（x）的解析式；（Ⅲ）将满足（Ⅱ）的函数f（x）的图象向右平移
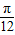个单位，纵坐标不变横坐标变为原来的2倍，再向下平移，得到函数g（x），求g（x）图象与x轴的正半轴、直线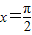所围成图形的面积．查看习题详情和答案>>
．
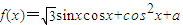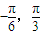]时，函数f（x）的最大值与最小值的和为
，求f（x）的解析式；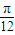
个单位，纵坐标不变横坐标变为原来的2倍，再向下平移
，得到函数g（x），求g（x）图象与x轴的正半轴、直线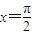
所围成图形的面积．
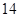分）设函数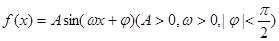
的最高点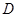
的坐标为（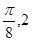
），由最高点
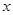的交点的坐标为（
）.
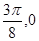的解析式.
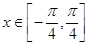时，求函数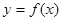
的图象向右平移
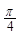个单位，得到函数
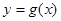的图象，求函数