网址:http://m.1010jiajiao.com/timu_id_435411[举报]
一、1~10 DBDAB DBCCB
二、11、2 ;12、2;13、.files/image244.gif) ;14、
;14、.files/image246.gif) ;15、伸长
;15、伸长 .files/image248.gif) ;伸长 6;左
;伸长 6;左 .files/image250.gif)
三、16 解:.files/image252.gif) ;
;.files/image254.gif) --------------6‘
--------------6‘
.files/image256.gif) ----------------------------------------8‘
----------------------------------------8‘
(或证.files/image258.gif) )
)
17解: (1) .files/image260.gif) ------------------- 3′
------------------- 3′
.files/image262.gif) 4′
4′
(2).files/image264.gif) 6′
6′
.files/image266.gif) 8′
8′
18.(1)记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,由题意知.files/image268.gif) 4′
4′
(2)ξ可取1,2,3,4. ξ的分布列为
ξ
1
2
3
4
P
.files/image061.gif)
.files/image271.gif)
.files/image273.gif)
.files/image275.gif)
7‘
.files/image277.gif) 8‘
8‘
19解: ⑴.files/image279.gif) 4‘
4‘
⑵.files/image281.gif)
.files/image283.gif) 6′
6′
.files/image285.gif)
.files/image287.gif) 7′
7′
.files/image289.gif) 8‘
8‘
20 解:(1)用反证法(略) 3‘
(2)根据函数图像分类,当.files/image291.gif) 时,
时,.files/image227.gif) 无最大值;当
无最大值;当.files/image294.gif) 时,
时,.files/image227.gif) 最大值,且
最大值,且.files/image297.gif) 的最大值为
的最大值为.files/image299.gif) ;
6‘
;
6‘
(3).files/image301.gif) ,
,.files/image303.gif) 7‘
7‘
.files/image305.gif) 8‘
8‘
已知数列 是首项为
是首项为 的等比数列,且满足
的等比数列,且满足
 .
.
(1) 求常数 的值和数列
的值和数列 的通项公式;
的通项公式;
(2) 若抽去数列 中的第一项、第四项、第七项、……、第
中的第一项、第四项、第七项、……、第 项、……,余下的项按原来的顺序组成一个新的数列
项、……,余下的项按原来的顺序组成一个新的数列 ,试写出数列
,试写出数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,设数列 的前
的前 项和为
项和为 .是否存在正整数
.是否存在正整数 ,使得
,使得 ?若存在,试求所有满足条件的正整数
?若存在,试求所有满足条件的正整数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问中解:由 得
得 ,,
,,
又因为存在常数p使得数列 为等比数列,
为等比数列,
则 即
即 ,所以p=1
,所以p=1
故数列 为首项是2,公比为2的等比数列,即
为首项是2,公比为2的等比数列,即 .
.
此时 也满足,则所求常数
也满足,则所求常数 的值为1且
的值为1且
第二问中,解:由等比数列的性质得:
(i)当 时,
时, ;
;
(ii) 当 时,
时, ,
,
所以
第三问假设存在正整数n满足条件,则 ,
,
则(i)当 时,
时,
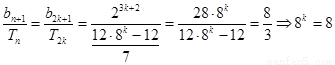
 ,
,
查看习题详情和答案>>
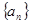 的首项为
的首项为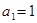 ,其前
,其前 项和为
项和为 ,且对任意正整数
,且对任意正整数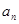 、
、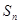 成等差数列.
成等差数列.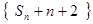 成等比数列;
成等比数列; 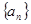 的首项为
的首项为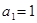 ,其前
,其前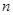 项和为
项和为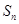 ,且对任意正整数
,且对任意正整数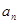 、
、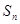 成等差数列.
成等差数列.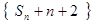 成等比数列;
成等比数列; 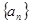 的首项为
的首项为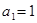 ,其前
,其前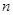 项和为
项和为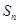 ,且对任意正整数
,且对任意正整数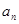 、
、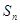 成等差数列.
成等差数列.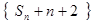 成等比数列;
成等比数列;  是首项为1的等差数列,其公差
是首项为1的等差数列,其公差 ,且
,且 、
、 、
、 成等比数列.
成等比数列. 的通项公式;
的通项公式;  项和为
项和为 ,求
,求 的最大值
的最大值