摘要：(2) .若在上最大值为0.最小值为-3.求与的值. 文科数学答案
网址：http://m.1010jiajiao.com/timu_id_432385[举报]
已知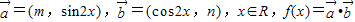
，若函数f（x）的图象经过点（0，1）和
．
（1）求m、n的值；
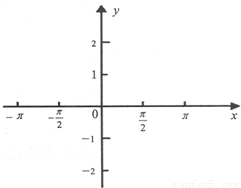
（2）用五点法画出f（x）在一个周期内的大致图象．
（3）若函数g（x）=af（x）+1在区间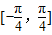
上的最大值与最小值之和为3，求a的值．
查看习题详情和答案>>
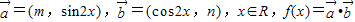，若函数f（x）的图象经过点（0，1）和．（1）求m、n的值；
（2）用五点法画出f（x）在一个周期内的大致图象．
（3）若函数g（x）=af（x）+1在区间
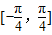上的最大值与最小值之和为3，求a的值．
查看习题详情和答案>>
探究函数
,x∈(0,+∞)的最小值，并确定相应的x的值，列表如下：
请观察表中y值随x值变化的特点，完成下列问题：
(1)若函数,(x>0)在区间(0,2)上递减，则在 上递增；
(2)当x= 时，,(x>0)的最小值为 ；
(3)试用定义证明,(x>0)在区间(0,2)上递减；
(4)函数,(x<0)有最值吗？是最大值还是最小值？此时x为何值？
（5）解不等式
.
解题说明：(1)(2)两题的结果直接填写在横线上；(4)题直接回答，不需证明。
,x∈(0,+∞)的最小值，并确定相应的x的值，列表如下：| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
(1)若函数
,(x>0)在区间(0,2)上递减，则在 上递增；(2)当x= 时，
,(x>0)的最小值为 ；(3)试用定义证明
,(x>0)在区间(0,2)上递减；(4)函数
,(x<0)有最值吗？是最大值还是最小值？此时x为何值？（5）解不等式
.解题说明：(1)(2)两题的结果直接填写在横线上；(4)题直接回答，不需证明。
已知点F（0，1），一动圆过点F且与圆x2+（y+1）2=8内切，
（1）求动圆圆心的轨迹C的方程；
（2）设点A（a，0），点P为曲线C上任一点，求点A到点P距离的最大值d（a）；
（3）在0＜a＜1的条件下，设△POA的面积为s1（O是坐标原点，P是曲线C上横坐标为a的点），以d（a）为边长的正方形的面积为s2．若正数m满足s1≤
ms2，问m是否存在最小值，若存在，请求出此最小值，若不存在，请说明理由．
查看习题详情和答案>>
（1）求动圆圆心的轨迹C的方程；
（2）设点A（a，0），点P为曲线C上任一点，求点A到点P距离的最大值d（a）；
（3）在0＜a＜1的条件下，设△POA的面积为s1（O是坐标原点，P是曲线C上横坐标为a的点），以d（a）为边长的正方形的面积为s2．若正数m满足s1≤
| 1 | 4 |
已知定点A