网址:http://m.1010jiajiao.com/timu_id_431460[举报]
一、选择题:本题考查基础的知识和基本运算,每题5分,满分60分。
二、填空题:本题考查基础知识和基本运算。每题4分,满分16分。
13.1 14.4 15.3 16.9+10+11,4+5+6+7+8,6+7+8+9(选对其中两个即可)
三、解答题:本题共6大题,共74分,解答应写出文字说明、证明过程或演算步骤。
17.本题主要考查三角函数的图像和性质,以及三角变换的知识,考查运算求解能力。
解:(I)由图象知.files/image233.gif)
将.files/image235.gif) 代入
代入.files/image237.gif) 得
得.files/image239.gif)
因为.files/image241.gif) ,所以
,所以.files/image243.gif)
所以.files/image245.gif)
(II)因为.files/image247.gif) 所以
所以.files/image249.gif)
.files/image251.gif)
.files/image253.gif) ,
,
.files/image255.gif)
.files/image257.gif)
18.本题考查样本估计总体,古典概型,频率分布直方图等知识,考查数据处理能力和分析问题、解决问题的能力。
解:(I)百米成绩在.files/image259.gif) 内的频率为0.32
内的频率为0.32.files/image261.gif)
0.32.files/image263.gif)
.files/image265.gif) 估计该年段学生中百米成绩在
估计该年段学生中百米成绩在.files/image259.gif) 内的人数为320人。
内的人数为320人。
(II)设图中从左到右前3个组的频率分别为3x,8x,19x依题意,得
.files/image268.gif) ,
,.files/image270.gif)
设调查中随机抽取了n个学生的百米成绩,则.files/image272.gif)
.files/image274.gif)
.files/image265.gif) 调查中随机抽取了50个学生的百米成绩。
调查中随机抽取了50个学生的百米成绩。
(III)百米成绩在第一组的学生数有.files/image277.gif) ,记他们的成绩为
,记他们的成绩为.files/image279.gif)
百米成绩在第五组的学生数由.files/image281.gif) ,记他们的成绩为
,记他们的成绩为.files/image283.gif)
则从第一、五组中随机取出两个成绩包含的基本事件有
.files/image285.gif)
其中满足成绩的差的绝对值大于1秒所包含的基本事件有
.files/image287.gif)
所以.files/image289.gif)
19.本题主要考查线面平行与垂直关系,及多面体的体积计算等基础知识,考察空间想象能力、抽象概括能力和运算求解能力。
(I)证明:取.files/image291.gif) 的重点P,连
的重点P,连.files/image293.gif)
.files/image295.gif) 已知M为CB中点,
已知M为CB中点,.files/image297.gif) ,且
,且.files/image299.gif)
由三视图可知,四边形.files/image301.gif) 为直角梯形,
为直角梯形,.files/image303.gif)
.files/image305.gif) ,
,.files/image265.gif) 四边形ANPM为平行四边形,
四边形ANPM为平行四边形,.files/image308.gif) ,
,
又.files/image310.gif) 平面
平面.files/image312.gif) 平面
平面.files/image314.gif) ,
,.files/image316.gif) 平面
平面.files/image314.gif)
(II).files/image295.gif) 该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,
该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,
.files/image319.gif) 两两垂直
两两垂直
.files/image265.gif)
.files/image322.gif) 与BA相交于B,
与BA相交于B,
.files/image324.gif) 平面
平面.files/image326.gif) ,BC为三棱锥
,BC为三棱锥.files/image328.gif) 的高
的高
.files/image330.jpg) 取
取.files/image332.gif) 的重点
的重点.files/image334.gif) ,连
,连.files/image336.gif) ,
,.files/image295.gif) 四边形
四边形.files/image301.gif) 的直角梯形且
的直角梯形且
.files/image340.gif) ,四边形ABQN为正方形,
,四边形ABQN为正方形,.files/image342.gif) ,
,
又.files/image344.gif) 平面
平面.files/image301.gif) ,
,.files/image346.gif) 平面
平面.files/image301.gif)
.files/image348.gif) ,
,
且.files/image350.gif) 与
与.files/image332.gif) 相交于B,
相交于B,.files/image353.gif) 平面
平面.files/image355.gif)
.files/image357.gif) 为四棱锥
为四棱锥.files/image359.gif) 的体积
的体积.files/image361.gif)
.files/image363.gif)
20.本题主要考查数列的该概念、等差数列、等比数列的通项及前n项和等基础知识,考察推理论证能力、函数与方程思想以及分类与整合思想
解:(I).files/image365.gif) 时,
时,.files/image367.gif)
.files/image369.gif) 时,
时,.files/image371.gif)
.files/image373.gif)
.files/image375.gif)
.files/image377.gif)
.files/image379.gif) 不是等比数列
不是等比数列
(II).files/image381.gif) ,
,
.files/image383.gif)
所以当.files/image385.gif) 时有:
时有:.files/image387.gif)
当.files/image389.gif) 时有:
时有:.files/image391.gif) ;
;
.files/image393.gif) 的最小值为
的最小值为.files/image395.gif)
(注:作商比较也可)
21.本题主要考查直线与椭圆的位置关系等基础知识,考察运算求解能力及化归与转换和数形结合思想。
解:(I)由题意椭圆的长轴.files/image397.gif) ,
,
.files/image399.gif) 在椭圆上,
在椭圆上,.files/image401.gif)
.files/image265.gif) 椭圆的方程为
椭圆的方程为.files/image404.gif)
(II)由直线l与圆O相切得.files/image406.gif)
设.files/image408.gif) ,由
,由.files/image410.gif) 消去
消去.files/image412.gif) ,整理得
,整理得.files/image414.gif)
由题可知圆O在椭圆内,所以直线必与椭圆相交,.files/image416.gif)
.files/image418.gif)
.files/image420.gif)
.files/image422.gif)
.files/image424.gif)
.files/image426.gif)
.files/image428.gif) 的值为
的值为.files/image430.gif)
22.本题主要考查函数与倒数的基本知识及综合应用知识的能力,考察分类与整合思想、化归与转换思想,考察分析问题和解决问题的能力。
解:(I)由已知得,.files/image432.gif)
.files/image295.gif) 函数
函数.files/image435.gif) 的单调递减区间是(1,2),
的单调递减区间是(1,2),.files/image437.gif) 的解是
的解是
.files/image439.gif)
.files/image441.gif) 的两个根本分别是1和2,且
的两个根本分别是1和2,且.files/image443.gif)
从.files/image445.gif) 且
且.files/image443.gif) ,可得
,可得.files/image448.gif)
又.files/image450.gif) 得
得.files/image452.gif)
.files/image454.gif)
(II)由(I)得,.files/image456.gif)
.files/image458.gif) 时,
时,.files/image460.gif) 在
在.files/image462.gif) 上是增函数,
上是增函数,
对.files/image464.gif) 当x=2时,
当x=2时,.files/image466.gif)
要使.files/image468.gif) 在
在.files/image470.gif) 上有解,
上有解,
即.files/image472.gif)
.files/image474.gif) 既
既.files/image476.gif) 对任意
对任意.files/image478.gif) 恒成立,
恒成立,
即.files/image480.gif) 对任意
对任意.files/image478.gif) 恒成立,
恒成立,
设.files/image483.gif) ,则
,则.files/image485.gif)
.files/image487.gif) 令
令.files/image489.gif) 得
得.files/image491.gif) 或
或.files/image493.gif)
在.files/image495.gif) 的符号与
的符号与.files/image497.gif) 德单调情况如下表:
德单调情况如下表:
m
(0,1)
1
(1,2)
.files/image499.gif)
-
0
+
.files/image497.gif)
æ
极小值
.files/image502.gif) ä
ä
.files/image504.gif) 时,
时,.files/image506.gif)
.files/image508.gif)
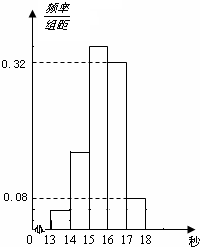 为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.(Ⅰ)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(Ⅱ)求调查中随机抽取了多少个学生的百米成绩;
(Ⅲ)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率. 查看习题详情和答案>>
为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图3所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
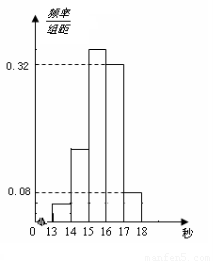
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.
查看习题详情和答案>>
为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.

查看习题详情和答案>>