摘要：当n≥2时.有 ②当①-②并整理得
网址：http://m.1010jiajiao.com/timu_id_430262[举报]
已知数列{an}和{bn}满足：a1＝λ，an+1＝
an＋n－4，bn＝(－1)n(an－3n＋21)，中λ为实数，n为正整数．
(1)当a3＝0时，求λ的值；
(2)试判断数列{bn}是否为等比数列，并证明你的结论；
(3)设0＜a＜b，，Sn为数列{bn}的前n项和，是否存在实数λ，使得对任意正整数n，都有a＜Sn＜b？若存在，求λ的取值范围；若不存在，说明理由．
设二次函数f(x)＝(k－4)x2＋kx(k∈R)，对任意实数x，有f(x)≤6x＋2恒成立；数列{an}满足an+1＝f(an)．
(1)求函数f(x)的解析式；
(2)试写出一个区间(a，b)，使得当an∈(a，b)时，an+1∈(a，b)且数列{an}是递增数列，并说明理由；
(3)已知a1＝
，是否存在非零整数λ，使得对任意n∈N*，都有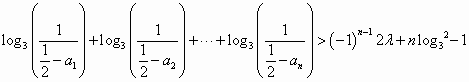
－1＋(－1)n－12λ＋nlog32恒成立，若存在，求之；若不存在，说明理由．
（本小题满分13分）
已知数列{an}中，a2＝p(p是不等于0的常数)，Sn为数列{an}的前n项和，若对任意的正整数n
都有Sn＝.
(1)证明：数列{an}为等差数列；(2)记
bn＝＋，求数列{bn}的前n项和Tn；
(3)记cn＝Tn－2n，是否存在正整数N，使得当n＞N时，恒有cn∈(，3)，若存在，请证明你的结论，并给出一个具体的N值；若不存在，请说明理由．