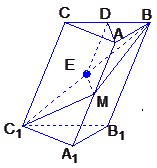
摘要：面∴AD⊥CC1. ------6(Ⅱ)延长B1A1与BM交于N, 连结C1N. ∵AM=MA1, ∴NA1=A1B1. ∵A1B1=A1C1, ∴A1C1= A1N=A1B1. ∴C1N⊥C1B1. ------9∵截面N B1C1⊥侧面BB1C1C,
网址：http://m.1010jiajiao.com/timu_id_430239[举报]
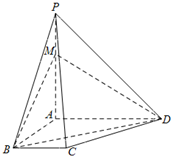四棱锥P-ABCD中，PA⊥底面ABCD，其中底面ABCD为梯形，AD∥BC，AB⊥BC，且AP=AB=AD=2BC=6，M在棱PA上，满足AM=2MP．（Ⅰ）求三棱锥M-BCD的体积；
（Ⅱ）求异面直线PC与AB所成角的余弦值；
（Ⅲ）证明：PC∥面MBD．
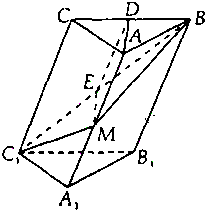在斜三棱柱A1B1C1-ABC中，底面是等腰三角形，AB=AC，侧面BB1C1C⊥底面ABC．（1）若D是BC的中点，求证：AD⊥CC1；
（2）过侧面BB1C1C的对角线BC1的平面交侧棱于M，若AM=MA1，求证：截面MBC1⊥侧面BB1C1C．
三棱柱ABC-A1B1C1中，面BB1C1C⊥面ABC，AB=AC，D是BC的中点，M为AA1上一动点．（1）求证：AD⊥CC1；
（2）若AM=MA1，求证：AD∥平面MBC1；
（3）若面MBC1⊥面BB1C1C，求证：AM=MA1．
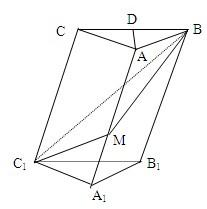在斜三棱柱A1B1C1-ABC中，底面是等腰三角形，AB=AC，侧面BB1C1C⊥底面ABC．