题目内容
 三棱柱ABC-A1B1C1中,面BB1C1C⊥面ABC,AB=AC,D是BC的中点,M为AA1上一动点.
三棱柱ABC-A1B1C1中,面BB1C1C⊥面ABC,AB=AC,D是BC的中点,M为AA1上一动点.(1)求证:AD⊥CC1;
(2)若AM=MA1,求证:AD∥平面MBC1;
(3)若面MBC1⊥面BB1C1C,求证:AM=MA1.
分析:(1)等腰△ABC中,中线AD⊥BC,结合线面垂直的性质定理,可得AD⊥面B1BCC1,从而AD⊥CC1;
(2)取BC的中点E,连接DE、ME.利用三角形中位线定理,结合平行四边形的性质,证出四边形ADEM是平行四边形,从而AD∥EM,可得AD∥平面MBC1;
(3)过点M作ME⊥BC1,垂足为E,连接EM.由线面垂直的性质定理,可得ME⊥面BB1C1C,结合AD⊥面B1BCC1,得ME∥AD.再根据线面平行的性质定理,证出DE∥AM,从而四边形ADEM是平行四边形.由此可得AM=DE=
CC1=
AA1,故AM=MA1.
(2)取BC的中点E,连接DE、ME.利用三角形中位线定理,结合平行四边形的性质,证出四边形ADEM是平行四边形,从而AD∥EM,可得AD∥平面MBC1;
(3)过点M作ME⊥BC1,垂足为E,连接EM.由线面垂直的性质定理,可得ME⊥面BB1C1C,结合AD⊥面B1BCC1,得ME∥AD.再根据线面平行的性质定理,证出DE∥AM,从而四边形ADEM是平行四边形.由此可得AM=DE=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵AB=AC,D为BC中点,∴AD⊥BC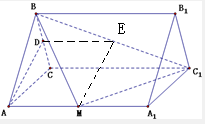
又∵面B1BCC1⊥面ABC,面B1BCC1∩面ABC=BC
∴AD⊥面B1BCC1,
又∵CC1?面B1BCC1,∴AD⊥CC1;
(2)取BC的中点E,连接DE、ME
∵△CC1B中,DE是中位线
∴DE∥CC1,且DE=
CC1,
又∵平行四边形AA1C1C中,M是AA1中点
∴AM∥CC1,且AM=
CC1,
∴DE∥AM且DE=AM,可得四边形ADEM是平行四边形
∴AD∥EM,
∵AD?平面MBC1且EM⊆平面MBC1
∴AD∥平面MBC1;
(3)过点M作ME⊥BC1,垂足为E,连接EM
∵面MBC1⊥面BB1C1C,面MBC1∩面BB1C1C=BC1,ME⊥BC1,
∴ME⊥面BB1C1C,
∵AB=AC,D为BC中点,∴AD⊥BC
又∵面B1BCC1⊥面ABC,面B1BCC1∩面ABC=BC
∴AD⊥面B1BCC1,可得ME∥AD
设AD、EM确定的平面为α,
∵AM∥面BB1C1C,AM⊆α,α∩面BB1C1C=DE,
∴DE∥AM
∴四边形ADEM是平行四边形,可得AM=DE
∵△BCC1中,DE∥CC1且D为BC的中点,∴DE=
CC1,
因此,可得AM=
CC1=
AA1,故AM=MA1.

又∵面B1BCC1⊥面ABC,面B1BCC1∩面ABC=BC
∴AD⊥面B1BCC1,
又∵CC1?面B1BCC1,∴AD⊥CC1;
(2)取BC的中点E,连接DE、ME
∵△CC1B中,DE是中位线
∴DE∥CC1,且DE=
| 1 |
| 2 |
又∵平行四边形AA1C1C中,M是AA1中点
∴AM∥CC1,且AM=
| 1 |
| 2 |
∴DE∥AM且DE=AM,可得四边形ADEM是平行四边形
∴AD∥EM,
∵AD?平面MBC1且EM⊆平面MBC1
∴AD∥平面MBC1;
(3)过点M作ME⊥BC1,垂足为E,连接EM
∵面MBC1⊥面BB1C1C,面MBC1∩面BB1C1C=BC1,ME⊥BC1,
∴ME⊥面BB1C1C,
∵AB=AC,D为BC中点,∴AD⊥BC
又∵面B1BCC1⊥面ABC,面B1BCC1∩面ABC=BC
∴AD⊥面B1BCC1,可得ME∥AD
设AD、EM确定的平面为α,
∵AM∥面BB1C1C,AM⊆α,α∩面BB1C1C=DE,
∴DE∥AM
∴四边形ADEM是平行四边形,可得AM=DE
∵△BCC1中,DE∥CC1且D为BC的中点,∴DE=
| 1 |
| 2 |
因此,可得AM=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题给出特殊三棱锥,求证线面平行和线面垂直.着重考查了线面平行的判定与性质,线面垂直、面面垂直的性质与判定等知识,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=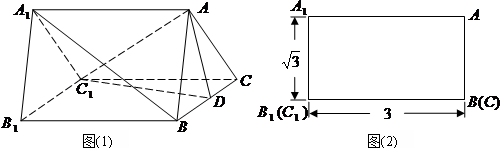
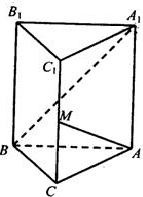 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1, 如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.
如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.