摘要：(1)证明:过点M作MH⊥AD于H.MG⊥AB于G.连结AM.∵M是正方形ABCD的对称中心.∴O是正方形ABCD对角线的交点.∴AM平分∠BAD.∴MH=MG. ∵正方形ABCD.QMNP.∴∠A=∠EMF=90°. ∴∠HMG=90°.∴∠EMG=∠HMF. ∴∠EMG=∠FMH.∵∠ MHF=∠MGE. ∴△MHF≌△MGE.∴ME=MF.(2)结论仍成立,(3)ME=mMF证明:过点M作MG⊥AD于G.MH⊥AB于H,∵∠EMF=∠B, ∴∠A=∠EMF=900,又∵∠MHA=∠MGA=900,∴∠HMG=900, ∴∠HMG=∠EMF∴∠FMG=∠EMH
网址：http://m.1010jiajiao.com/timu_id_429723[举报]
如图，Rt△ACB和Rt△BAD中，∠ACB=∠BDA=90°，∠ABC=∠BAD，边AD与BC相交于点E．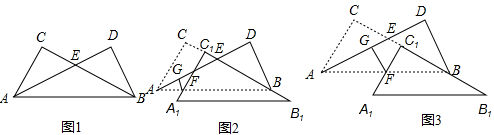
（1）在图1中，求证：AC=BD；
（2）当Rt△ACB沿BC方向平移到图2所示位置时，边A1C1与AB边交于点F．过点F作FG⊥AD于点G．此时请你通过观察、测量和猜想．写出FG+FC1与BD之间满足的数量关系，然后证明你的猜想；
（3）当Rt△ACB沿BC方向平移到图3所示的位置（点C1在线段BE上，且点C1与点B不重合）时，（2）中的猜想是否仍然成立？（不用说明理由）
查看习题详情和答案>>
（1）在图1中，求证：AC=BD；
（2）当Rt△ACB沿BC方向平移到图2所示位置时，边A1C1与AB边交于点F．过点F作FG⊥AD于点G．此时请你通过观察、测量和猜想．写出FG+FC1与BD之间满足的数量关系，然后证明你的猜想；
（3）当Rt△ACB沿BC方向平移到图3所示的位置（点C1在线段BE上，且点C1与点B不重合）时，（2）中的猜想是否仍然成立？（不用说明理由）
如图，Rt△ACB和Rt△BAD中，∠ACB=∠BDA=90°，∠ABC=∠BAD，边AD与BC相交于点E．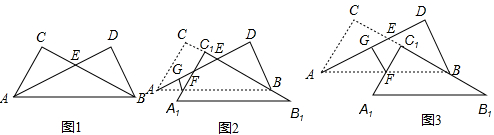
（1）在图1中，求证：AC=BD；
（2）当Rt△ACB沿BC方向平移到图2所示位置时，边A1C1与AB边交于点F．过点F作FG⊥AD于点G．此时请你通过观察、测量和猜想．写出FG+FC1与BD之间满足的数量关系，然后证明你的猜想；
（3）当Rt△ACB沿BC方向平移到图3所示的位置（点C1在线段BE上，且点C1与点B不重合）时，（2）中的猜想是否仍然成立？（不用说明理由）
查看习题详情和答案>>
如图，Rt△ACB和Rt△BAD中，∠ACB=∠BDA=90°，∠ABC=∠BAD，边AD与BC相交于点E．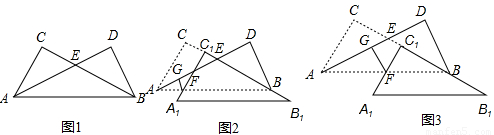
（1）在图1中，求证：AC=BD；
（2）当Rt△ACB沿BC方向平移到图2所示位置时，边A1C1与AB边交于点F．过点F作FG⊥AD于点G．此时请你通过观察、测量和猜想．写出FG+FC1与BD之间满足的数量关系，然后证明你的猜想；
（3）当Rt△ACB沿BC方向平移到图3所示的位置（点C1在线段BE上，且点C1与点B不重合）时，（2）中的猜想是否仍然成立？（不用说明理由）
查看习题详情和答案>>
（1）在图1中，求证：AC=BD；
（2）当Rt△ACB沿BC方向平移到图2所示位置时，边A1C1与AB边交于点F．过点F作FG⊥AD于点G．此时请你通过观察、测量和猜想．写出FG+FC1与BD之间满足的数量关系，然后证明你的猜想；
（3）当Rt△ACB沿BC方向平移到图3所示的位置（点C1在线段BE上，且点C1与点B不重合）时，（2）中的猜想是否仍然成立？（不用说明理由）
查看习题详情和答案>>
（2012•烟台）如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）．以A为顶点的抛物线y=ax2+bx+c过点C．动点P从点A出发，沿线段AB向点B运动．同时动点Q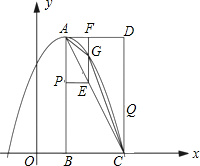
从点C出发，沿线段CD向点D运动．点P，Q的运动速度均为每秒1个单位．运动时间为t秒．过点P作PE⊥AB交AC于点E．
（1）直接写出点A的坐标，并求出抛物线的解析式；
（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？
（3）在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．
查看习题详情和答案>>
从点C出发，沿线段CD向点D运动．点P，Q的运动速度均为每秒1个单位．运动时间为t秒．过点P作PE⊥AB交AC于点E．（1）直接写出点A的坐标，并求出抛物线的解析式；
（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？
（3）在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．
（2012•铁岭）如图，在平面直角坐标系中，四边形ABCD是梯形，BC∥AD，∠BAD+∠CDA=90°，且tan∠BAD=2，AD在x轴上，点A的坐标（-1，0），点B在y轴的正半轴上，BC=OB．
（1）求过点A、B、C的抛物线的解析式；
（2）动点E从点B（不包括点B）出发，沿BC运动到点C停止，在运动过程中，过点E作EF⊥AD于点F，将四边形ABEF沿直线EF折叠，得到四边形A1B1EF，点A、B的对应点分别是点A1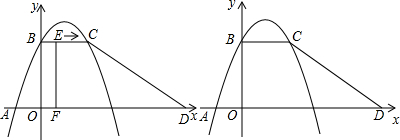
、B1，设四边形A1B1EF与梯形ABCD重合部分的面积为S，F点的坐标是（x，0）．
①当点A1落在（1）中的抛物线上时，求S的值；
②在点E运动过程中，求S与x的函数关系式．
查看习题详情和答案>>
（1）求过点A、B、C的抛物线的解析式；
（2）动点E从点B（不包括点B）出发，沿BC运动到点C停止，在运动过程中，过点E作EF⊥AD于点F，将四边形ABEF沿直线EF折叠，得到四边形A1B1EF，点A、B的对应点分别是点A1
、B1，设四边形A1B1EF与梯形ABCD重合部分的面积为S，F点的坐标是（x，0）．①当点A1落在（1）中的抛物线上时，求S的值；
②在点E运动过程中，求S与x的函数关系式．