题目内容
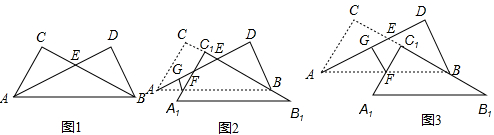
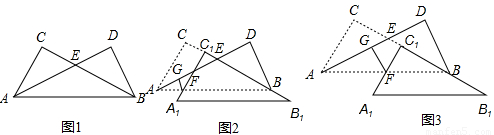
如图,Rt△ACB和Rt△BAD中,∠ACB=∠BDA=90°,∠ABC=∠BAD,边AD与BC相交于点E.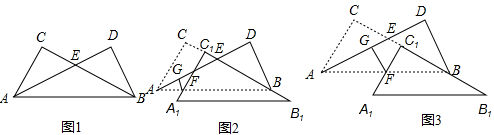
(1)在图1中,求证:AC=BD;
(2)当Rt△ACB沿BC方向平移到图2所示位置时,边A1C1与AB边交于点F.过点F作FG⊥AD于点G.此时请你通过观察、测量和猜想.写出FG+FC1与BD之间满足的数量关系,然后证明你的猜想;
(3)当Rt△ACB沿BC方向平移到图3所示的位置(点C1在线段BE上,且点C1与点B不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)

(1)在图1中,求证:AC=BD;
(2)当Rt△ACB沿BC方向平移到图2所示位置时,边A1C1与AB边交于点F.过点F作FG⊥AD于点G.此时请你通过观察、测量和猜想.写出FG+FC1与BD之间满足的数量关系,然后证明你的猜想;
(3)当Rt△ACB沿BC方向平移到图3所示的位置(点C1在线段BE上,且点C1与点B不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)
分析:(1)由已知的两对角相等,加上公共边AB=BA,利用AAS得出三角形ABC与三角形ABD全等,由全等三角形的对应边相等即可得证;
(2)FG+FC1=BD;理由为:过F作FH垂直于BD,由三个角为直角的四边形为矩形得到GFHD为矩形,可得FG=DH,DG与FH平行,由平行得到一对同位角相等,再由平移的性质及已知的两角相等得到一对角相等,再由一对直角相等及FB为公共边,利用AAS可得出三角形C1FB与三角形HBF全等,由全等三角形的对应边相等得到C1F=HB,等量代换即可得证;
(3)当Rt△ACB沿BC方向平移到图3所示的位置(点C1在线段BE上,且点C1与点B不重合)时,(2)中的猜想仍然成立,证明方法同理.
(2)FG+FC1=BD;理由为:过F作FH垂直于BD,由三个角为直角的四边形为矩形得到GFHD为矩形,可得FG=DH,DG与FH平行,由平行得到一对同位角相等,再由平移的性质及已知的两角相等得到一对角相等,再由一对直角相等及FB为公共边,利用AAS可得出三角形C1FB与三角形HBF全等,由全等三角形的对应边相等得到C1F=HB,等量代换即可得证;
(3)当Rt△ACB沿BC方向平移到图3所示的位置(点C1在线段BE上,且点C1与点B不重合)时,(2)中的猜想仍然成立,证明方法同理.
解答: (1)证明:在Rt△ACB和Rt△BDA中,
(1)证明:在Rt△ACB和Rt△BDA中,
,
∴△ACB≌△BDA(AAS),
∴AC=BD;
(2)FG+FC1=BD;理由为:
证明:过点F作FH⊥BD于点H(如图2),
∵FG⊥AD于点G,∠D=90°,
∴四边形FGDH为矩形,
∴FG=HD,DG∥FH,
∴∠DAB=∠HFB,
∵∠DAB=∠CBA,
∴∠CBA=∠HFB,
在△C1FB≌△HBF中,
∴△C1FB≌△HBF(AAS),
∴C1F=HB,
∴GF+C1F=DH+HB=BD,即FG+FC1=BD;
(3)仍然成立.关系式为FG+FC1=BD,理由为:
证明:过点F作FH⊥BD于点H(如图3),
∵FG⊥AD于点G,∠D=90°,
∴四边形FGDH为矩形,
∴FG=HD,DG∥FH
∴∠DAB=∠HFB,
∵∠DAB=∠CBA,
∴∠CBA=∠HFB,
在△C1FB≌△HBF中,
∴△C1FB≌△HBF(AAS),
∴C1F=HB,
∴GF+C1F=DH+HB=BD,即FG+FC1=BD.
 (1)证明:在Rt△ACB和Rt△BDA中,
(1)证明:在Rt△ACB和Rt△BDA中,
|
∴△ACB≌△BDA(AAS),
∴AC=BD;
(2)FG+FC1=BD;理由为:
证明:过点F作FH⊥BD于点H(如图2),
∵FG⊥AD于点G,∠D=90°,
∴四边形FGDH为矩形,
∴FG=HD,DG∥FH,
∴∠DAB=∠HFB,
∵∠DAB=∠CBA,
∴∠CBA=∠HFB,
在△C1FB≌△HBF中,
|
∴△C1FB≌△HBF(AAS),
∴C1F=HB,
∴GF+C1F=DH+HB=BD,即FG+FC1=BD;
(3)仍然成立.关系式为FG+FC1=BD,理由为:
证明:过点F作FH⊥BD于点H(如图3),
∵FG⊥AD于点G,∠D=90°,
∴四边形FGDH为矩形,
∴FG=HD,DG∥FH
∴∠DAB=∠HFB,
∵∠DAB=∠CBA,
∴∠CBA=∠HFB,
在△C1FB≌△HBF中,
|
∴△C1FB≌△HBF(AAS),
∴C1F=HB,
∴GF+C1F=DH+HB=BD,即FG+FC1=BD.
点评:此题考查了全等三角形的判定与性质,平移的性质,以及矩形的判额定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
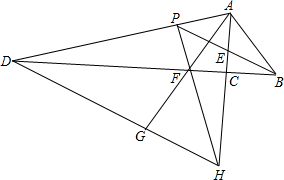 如图,Rt△ACB中,∠ACB=90°,∠ABC的角平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD-AH=AB;④DG=AP+GH.其中正确的是( )
如图,Rt△ACB中,∠ACB=90°,∠ABC的角平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD-AH=AB;④DG=AP+GH.其中正确的是( )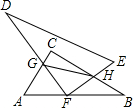 如图,Rt△ABC和Rt△DEF中,∠ACB=∠DFE=90°,F为AB的中点,DF与AC交于点G,EF与BC交于点H,则AG、BH、GH满足的等量关系为
如图,Rt△ABC和Rt△DEF中,∠ACB=∠DFE=90°,F为AB的中点,DF与AC交于点G,EF与BC交于点H,则AG、BH、GH满足的等量关系为