题目内容
(2012•铁岭)如图,在平面直角坐标系中,四边形ABCD是梯形,BC∥AD,∠BAD+∠CDA=90°,且tan∠BAD=2,AD在x轴上,点A的坐标(-1,0),点B在y轴的正半轴上,BC=OB.
(1)求过点A、B、C的抛物线的解析式;
(2)动点E从点B(不包括点B)出发,沿BC运动到点C停止,在运动过程中,过点E作EF⊥AD于点F,将四边形ABEF沿直线EF折叠,得到四边形A1B1EF,点A、B的对应点分别是点A1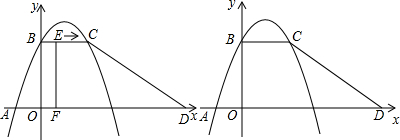 、B1,设四边形A1B1EF与梯形ABCD重合部分的面积为S,F点的坐标是(x,0).
、B1,设四边形A1B1EF与梯形ABCD重合部分的面积为S,F点的坐标是(x,0).
①当点A1落在(1)中的抛物线上时,求S的值;
②在点E运动过程中,求S与x的函数关系式.
(1)求过点A、B、C的抛物线的解析式;
(2)动点E从点B(不包括点B)出发,沿BC运动到点C停止,在运动过程中,过点E作EF⊥AD于点F,将四边形ABEF沿直线EF折叠,得到四边形A1B1EF,点A、B的对应点分别是点A1
 、B1,设四边形A1B1EF与梯形ABCD重合部分的面积为S,F点的坐标是(x,0).
、B1,设四边形A1B1EF与梯形ABCD重合部分的面积为S,F点的坐标是(x,0).①当点A1落在(1)中的抛物线上时,求S的值;
②在点E运动过程中,求S与x的函数关系式.
分析:(1)根据条件先求出B点和C点的坐标,再利用待定系数法就可以求出过点A、B、C的抛物线的解析式.
(2)①根据抛物线的对称性可以知道当点A1落在抛物线上A1与点A关于对称轴对称,重合部分面积就是梯形ABEF的面积.从而求出S的值.
②从0<x≤1和当1<x≤2两种情况分别把点E在运动的过程中重叠部分的面积表示出来,当0<x≤1时重叠部分的面积就是梯形ABEF的面积,当1<x≤2时,重叠部分的面积就是一个五边形的面积.就是一个梯形的面积减去一个三角形
的面积就可以了.
(2)①根据抛物线的对称性可以知道当点A1落在抛物线上A1与点A关于对称轴对称,重合部分面积就是梯形ABEF的面积.从而求出S的值.
②从0<x≤1和当1<x≤2两种情况分别把点E在运动的过程中重叠部分的面积表示出来,当0<x≤1时重叠部分的面积就是梯形ABEF的面积,当1<x≤2时,重叠部分的面积就是一个五边形的面积.就是一个梯形的面积减去一个三角形
的面积就可以了.
解答:解:(1)∵点A坐标是(-1,0),
∴OA=1,
在△ABO中∠AOB=90°tanA=
=2,
∴OB=2.
∴点B的坐标是(0,2).
∵BC∥AD,BC=OB,
∴BC=2,
∴点C的坐标是(2,2).
设抛物线表达式为y=ax2+bx+2,由题意,得
∴
∴解得
∴y=-
x2+
x+2.
(2)①当点A1落在抛物线上,根据抛物线的轴对称性可得A1与点A关于对称轴对称,
由沿直线EF折叠,所以点E是BC上一个点,
重合部分面积就是梯形ABEF的面积.
∴S=S梯形ABEF=
(BE+AF)×BO=2+1=3;
②当0<x≤1时,重合部分面积就是梯形ABEF的面积,
由题得AF=x+1,BE=x,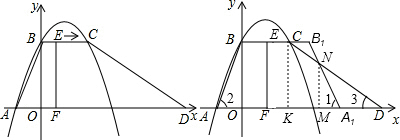
S=S梯形ABEF=
(BE+AF)×BO=2x+1.
当1<x≤2时,重合部分面积就是五边形A1NCEF的面积,
设A1B1交CD于点N,作MN⊥DF于点M,CK⊥AD于点K,
∴∠CKD=∠NMD=90°
由轴对称得:∠1=∠2,
∵∠2+∠3=90°,
∴∠1+∠3=90°,
∠3+∠MND=90°
∴∠MND=∠1
△NMA1∽△DMN,
=
,
∵∠BAO=∠MA1N,tan∠BAO=2,
∴tan∠MA1N=2=
.
∴2MA1=MN,MD=2MN.
∴MD=4MA1,
∴DA1=3MA1
∵tan∠BAO=2,∠BAO+∠CDK=90°,
∴tan∠CDK=
.
在△DCK中,∠CKD=90°,CK=OB=2,
tan∠CDK=
=
,
∴DK=4,OD=6.
∵OF=x,A1F=x+1,
∴A1D=OD-OF-A1F=5-2x,FD=6-x.
∴3MA1=5-2x,
∴MA1=
(5-2x)
∵2MA1=MN
∴MN=
(5-2x).
∴S=S梯形DCEF-S△A1ND=8-2x-
(5-2x)2=-
x2+
x-
.
∴OA=1,
在△ABO中∠AOB=90°tanA=
| OB |
| OA |
∴OB=2.
∴点B的坐标是(0,2).
∵BC∥AD,BC=OB,
∴BC=2,
∴点C的坐标是(2,2).
设抛物线表达式为y=ax2+bx+2,由题意,得
∴
|
∴解得
|
∴y=-
| 2 |
| 3 |
| 4 |
| 3 |
(2)①当点A1落在抛物线上,根据抛物线的轴对称性可得A1与点A关于对称轴对称,
由沿直线EF折叠,所以点E是BC上一个点,
重合部分面积就是梯形ABEF的面积.
∴S=S梯形ABEF=
| 1 |
| 2 |
②当0<x≤1时,重合部分面积就是梯形ABEF的面积,
由题得AF=x+1,BE=x,

S=S梯形ABEF=
| 1 |
| 2 |
当1<x≤2时,重合部分面积就是五边形A1NCEF的面积,
设A1B1交CD于点N,作MN⊥DF于点M,CK⊥AD于点K,
∴∠CKD=∠NMD=90°
由轴对称得:∠1=∠2,
∵∠2+∠3=90°,
∴∠1+∠3=90°,
∠3+∠MND=90°
∴∠MND=∠1
△NMA1∽△DMN,
| MA1 |
| NM |
| NM |
| MD |
∵∠BAO=∠MA1N,tan∠BAO=2,
∴tan∠MA1N=2=
| MN |
| A1M |
∴2MA1=MN,MD=2MN.
∴MD=4MA1,
∴DA1=3MA1
∵tan∠BAO=2,∠BAO+∠CDK=90°,
∴tan∠CDK=
| 1 |
| 2 |
在△DCK中,∠CKD=90°,CK=OB=2,
tan∠CDK=
| CK |
| DK |
| 1 |
| 2 |
∴DK=4,OD=6.
∵OF=x,A1F=x+1,
∴A1D=OD-OF-A1F=5-2x,FD=6-x.
∴3MA1=5-2x,
∴MA1=
| 1 |
| 3 |
∵2MA1=MN
∴MN=
| 2 |
| 3 |
∴S=S梯形DCEF-S△A1ND=8-2x-
| 1 |
| 3 |
| 4 |
| 3 |
| 14 |
| 3 |
| 1 |
| 3 |
点评:本题是一道二次函数的综合试题,考查了待定系数法求函数的解析式,梯形的面积公式,动点问题在函数解析式中的运用.相似三角形的判定及性质的运用.

练习册系列答案
相关题目
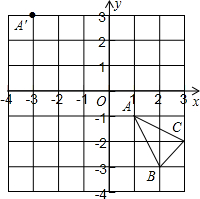 (2012•铁岭)如图,在平面直角坐标系中,△ABC经过平移后点A的对应点为点A′,则平移后点B的对应点B′的坐标为
(2012•铁岭)如图,在平面直角坐标系中,△ABC经过平移后点A的对应点为点A′,则平移后点B的对应点B′的坐标为 (2012•铁岭)如图,点E、F、G、H分别为菱形A1B1C1D1各边的中点,连接A1F、B1G、C1H、D1E得四边形A2B2C2D2,以此类推得四边形A3B3C3D3…,若菱形A1B1C1D1的面积为S,则四边形AnBnCnDn的面积为
(2012•铁岭)如图,点E、F、G、H分别为菱形A1B1C1D1各边的中点,连接A1F、B1G、C1H、D1E得四边形A2B2C2D2,以此类推得四边形A3B3C3D3…,若菱形A1B1C1D1的面积为S,则四边形AnBnCnDn的面积为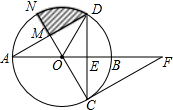 (2012•铁岭)如图,AB为⊙O的直径,弦CD垂直平分OB于点E,点F在AB延长线上,∠AFC=30°.
(2012•铁岭)如图,AB为⊙O的直径,弦CD垂直平分OB于点E,点F在AB延长线上,∠AFC=30°.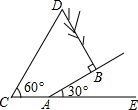 (2012•铁岭)如图,在斜坡AB上有一棵树BD,由于受台风影响而倾斜,恰好与坡面垂直,在地面上C点处测得树顶部D的仰角为60°,测得坡角∠BAE=30°,AB=6米,AC=4米.求树高BD的长是多少米?(结果保留根号)
(2012•铁岭)如图,在斜坡AB上有一棵树BD,由于受台风影响而倾斜,恰好与坡面垂直,在地面上C点处测得树顶部D的仰角为60°,测得坡角∠BAE=30°,AB=6米,AC=4米.求树高BD的长是多少米?(结果保留根号)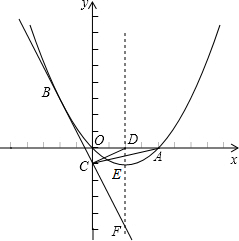 -2x-1经过抛物线上一点B(-2,m)且与y轴交于点C,与抛物线的对称轴交于点F.
-2x-1经过抛物线上一点B(-2,m)且与y轴交于点C,与抛物线的对称轴交于点F.