摘要:18.解: 1)过点D作DE ⊥ A1 C 于E点.取AC的中点F.连BF ?EF.∵面DA1 C⊥面AA1C1C且相交于A1 C.面DA1 C内的直线DE ⊥ A1 C∴直线DE⊥面AA1C1C ---3分又∵面BA C⊥面AA1C1C且相交于AC.易知BF⊥AC.∴BF⊥面AA1C1C由此知:DE∥BF .从而有D.E.F.B共面.又易知BB1∥面AA1C1C.故有DB∥EF .从而有EF∥AA1.
网址:http://m.1010jiajiao.com/timu_id_42724[举报]
 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A.(几何证明选讲)
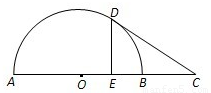
如图,AB是半圆的直径,C是AB延长线上一点,CD切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是OB的中点,求BC的长.
B.(矩阵与变换)
已知矩阵
|
|
C.(极坐标与参数方程)
在平面直角坐标系xOy中,已知点A(1,-2)在曲线
|
D.(不等式选讲)
设a1,a2,a3均为正数,且a1+a2+a3=1,求证:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
 的属于特征值b的一个特征向量为
的属于特征值b的一个特征向量为 ,求实数a、b的值.
,求实数a、b的值. (t为参数,p为正常数),求p的值.
(t为参数,p为正常数),求p的值.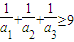 .
.