摘要：若0≤≤1.当cosx＝时.f (x)取得最小值-22-1.由题意有-22-1＝-7.得＝±.
网址：http://m.1010jiajiao.com/timu_id_42711[举报]
已知向量
=(cos(x-
)，sin(x-
))，
=(cos(x+
)，-sin(x+
))，f(x)=
•
-k|
+
|，x∈[0，π]．
（1）若x=
，求
•
及|
+
|；
（2）若k=1，当x为何值时，f（x）有最小值，最小值是多少？
（3）若f（x）的最大值为3，求k的值． 查看习题详情和答案>>
| a |
| π |
| 4 |
| π |
| 4 |
| b |
| π |
| 4 |
| π |
| 4 |
| a |
| b |
| a |
| b |
（1）若x=
| 7π |
| 12 |
| a |
| b |
| a |
| b |
（2）若k=1，当x为何值时，f（x）有最小值，最小值是多少？
（3）若f（x）的最大值为3，求k的值． 查看习题详情和答案>>
已知函数f（x）=4x3-3x2cosθ+
，其中x∈R，θ为参数，且0≤θ≤2π．
①当cosθ=0时，判断函数f（x）是否有极值；
②要使函数f（x）的极小值小于零，求参数θ的取值范围；
③若对②中所求的取值范围内的任意参数θ，函数f（x）在区间（2a-1，a）内都是增函数，求实数a的取值范围．
查看习题详情和答案>>
| 1 | 32 |
①当cosθ=0时，判断函数f（x）是否有极值；
②要使函数f（x）的极小值小于零，求参数θ的取值范围；
③若对②中所求的取值范围内的任意参数θ，函数f（x）在区间（2a-1，a）内都是增函数，求实数a的取值范围．
已知函数f（x）=4x3-3x2cosθ+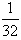
，其中x∈R，θ为参数，且0≤θ≤
，
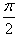（1）当cosθ=0时，判断函数f（x）是否有极值；
（2）要使函数f（x）的极小值大于零，求参数θ的取值范围；
（3）若对（2）中所求的取值范围内的任意参数θ，函数f（x）在区间（2a-1，a）内都是增函数，求实数a的取值范围。
查看习题详情和答案>>
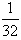，其中x∈R，θ为参数，且0≤θ≤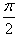，（1）当cosθ=0时，判断函数f（x）是否有极值；
（2）要使函数f（x）的极小值大于零，求参数θ的取值范围；
（3）若对（2）中所求的取值范围内的任意参数θ，函数f（x）在区间（2a-1，a）内都是增函数，求实数a的取值范围。
cosθ，其中x∈R，θ为参数，且0≤θ＜2π，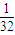
，其中x∈R，θ为参数，且0≤θ≤2π．