摘要:又因为|OP|=||=1.|OQ|=|z2ω3|=|z|2|ω|3=1∴|OP|=|OQ|.由此知△OPQ为等腰直角三角形.
网址:http://m.1010jiajiao.com/timu_id_425886[举报]
 在平面向量中有如下定理:设点O、P、Q、R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使
在平面向量中有如下定理:设点O、P、Q、R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使| OP |
| OQ |
| OR |
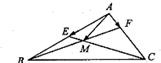
如图,在△ABC中,点E为AB边的中点,点F在AC边上,且CF=2FA,BF交CE于点M,设
| AM |
| AE |
| AF |
网址:http://m.1010jiajiao.com/timu_id_425886[举报]
 在平面向量中有如下定理:设点O、P、Q、R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使
在平面向量中有如下定理:设点O、P、Q、R为同一平面内的点,则P、Q、R三点共线的充要条件是:存在实数t,使| OP |
| OQ |
| OR |
| AM |
| AE |
| AF |