Question

已知|

OP

|=1，|

OQ

|=

3

，

OP

⊥

OQ

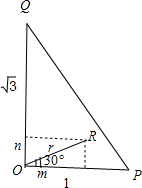
，点R在△POQ内，且∠POR=30°，设

OR

=m

OP

+n

OQ

 （m，n∈R），则

m

n

等于（　　）

• A、

  1

  3

• B、3
• C、

  3

  3

• D、

  3

Answer 1

分析：由题意可得

OQ

•

OP

=0，可得

OR

•

OP

=m•

OP

2，故有 m=rcos30°．再由

OR

•

OQ

=n•

OQ

2，可得3n=

3

rcos60°，从而求得

m

n

 的值．

解答：解：设|OR|=r，由于

OR

=m

OP

+n

OQ

，

OP

⊥

OQ

，∴

OQ

•

OP

=0，故

OR

•

OP

=m•

OP

2，∴m=rcos30°．
又∵

OR

•

OQ

=n•

OQ

2，∴

3

rcos60°=3n，故

m

n

=3，
故选B．

点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量的数量积的运算，属于中档题．