Question

在平面向量中有如下定理：设点O、P、Q、R为同一平面内的点，则P、Q、R三点共线的充要条件是：存在实数t，使

OP

=(1-t)

OQ

+t

OR

．试利用该定理解答下列问题：
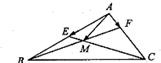
如图，在△ABC中，点E为AB边的中点，点F在AC边上，且CF=2FA，BF交CE于点M，设

AM

=x

AE

+y

AF

，则x+2y=

 

．

Answer 1

分析：题目中所给的定理，实际上是向量共线的定理的推论，我们要理解、应用它，可以看出B，M，F三点共线，直接应用结论，再根据中点得到两个向量之间的关系，得到结论．

解答：解：由题意知：B，M，F三点共线，
∴

AM

=(1-t)

AB

+t

AF

∵

AB

=2

AE

∴

AM

=2(I-t)

AE

+t

AF

∴x=2（1-t），y=t
∴x+2y=2
故答案为：2

点评：用一组向量来表示一个向量，是以后解题过程中常见到的，向量的加减运算是用向量解决问题的基础，要学好运算，才能用向量解决立体几何问题，三角函数问题，好多问题都是以向量为载体的．