摘要:∴由等比数列求和公式可得:∴1+z+z2+z3+-+z6=0解法二:S=1+z+z2+-+z6 ①zS=z+z2+z3+-+z6+z7 ②∴①-②得(1-z)S=1-z7=0
网址:http://m.1010jiajiao.com/timu_id_425782[举报]
在平面直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为
 点
点 是曲线
是曲线 上的动点.
上的动点.
(1)求线段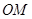 的中点
的中点 的轨迹的直角坐标方程;
的轨迹的直角坐标方程;
(2) 以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,若直线
轴的正半轴为极轴建立极坐标系,若直线 的极坐标方程为
的极坐标方程为 ,求点
,求点 到直线
到直线 距离的最大值.
距离的最大值.
【解析】第一问利用设曲线 上动点
上动点 ,由中点坐标公式可得
,由中点坐标公式可得
 所以点
所以点 的轨迹的参数方程为
的轨迹的参数方程为
 消参可得
消参可得
第二问,由题可知直线 的直角坐标方程为
的直角坐标方程为 ,因为原点到直线的距离为
,因为原点到直线的距离为 ,
,
所以点 到直线的最大距离为
到直线的最大距离为
查看习题详情和答案>>
已知在等比数列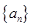 中,
中,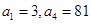 ,若数列
,若数列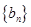 满足:
满足: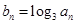 ,数列
,数列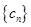 满足:
满足: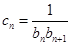 ,且数列
,且数列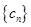 的前
的前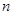 项和为
项和为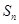 .
.
(1)求数列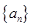 的通项公式; (2)求数列
的通项公式; (2)求数列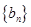 的通项公式; (3) 求
的通项公式; (3) 求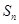 .
.
【解析】第一问∵ 在等比数列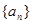 中,
中,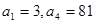 , ∴
, ∴ 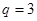
∴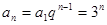
(2)中 ∵ 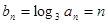
(3)中 由(2)可得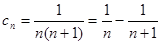 列项求和得到。
列项求和得到。
∴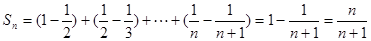
查看习题详情和答案>>
某批数量较大的商品的次品率是5%,从中任意地连续取出10件,![]() 为所含次品的个数,求
为所含次品的个数,求![]() .
.
分析:数量较大,意味着每次抽取时出现次品的概率都是0.05,![]() 可能取值是:0,1,2,…,10.10次抽取看成10次独立重复试验,所以抽到次品数
可能取值是:0,1,2,…,10.10次抽取看成10次独立重复试验,所以抽到次品数![]() 服从二项分布,由公式
服从二项分布,由公式![]() 可得解.
可得解.
