摘要：(Ⅰ)解:求f(x)的导数:f′(x)=3x2.由此得切线l的方程:y-(x13-a)=3x12(x-x1).(Ⅱ)证明:依题意.切线方程中令y=0.
网址：http://m.1010jiajiao.com/timu_id_425627[举报]
函数y=f（x）g（x）在求导数时，可以运用对数法：在函数解析式两边求对数得lny=g（x）lnf（x），两边求导数
=g′(x)lnf(x)+g(x)
，于是y'=f（x）g（x）[g′(x)lnf(x)+g(x)
]．运用此方法可以探求得知y=x
(x＞0)的一个单调增区间为 ．
查看习题详情和答案>>
| y′ |
| y |
| f′(x) |
| f(x) |
| f′(x) |
| f(x) |
| 1 |
| x |
函数y=f（x）g（x）在求导数时，可以运用对数法：在函数解析式两边求对数得lny=g（x）lnf（x），两边求导数
=g′(x)lnf(x)+g(x)
，于是y'=f（x）g（x）[g′(x)lnf(x)+g(x)
]．运用此方法可以探求得知y=x
(x＞0)的一个单调增区间为______．
查看习题详情和答案>>
| y′ |
| y |
| f′(x) |
| f(x) |
| f′(x) |
| f(x) |
| 1 |
| x |
函数y=f（x）g（x）在求导数时，可以运用对数法：在函数解析式两边求对数得lny=g（x）lnf（x），两边求导数
，于是y'=f（x）g（x）
．运用此方法可以探求得知
的一个单调增区间为 ．
查看习题详情和答案>>
，于是y'=f（x）g（x）．运用此方法可以探求得知的一个单调增区间为 ．
查看习题详情和答案>>
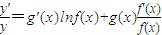，于是y'=f（x）g（x）
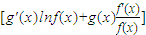．运用此方法可以探求得知
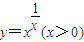的一个单调增区间为 ．
，于是y'=f（x）g（x）
．运用此方法可以探求得知
的一个单调增区间为 ．