我们为了探究函数  的部分性质，先列表如下：

请你观察表中y值随x值变化的特点，完成以下的问题.

首先比较容易的看出来：此函数在区间（0，2）上是递减的；

（1）函数在区间                      上递增.

当              时，               .

（2）请你根据上面性质作出此函数的大概图像；

（3）证明：此函数在区间上（0，2）是递减的.

我们为了探究函数 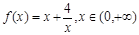 的部分性质，先列表如下：

在棱长为的正方体中,是线段的中点,.

(1) 求证:^；

(2) 求证://平面；

(3) 求三棱锥的表面积.

【解析】本试题考查了线线垂直和线面平行的判定定理和表面积公式的运用。第一问中，利用，得到结论，第二问中，先判定为平行四边形，然后，可知结论成立。

第三问中，是边长为的正三角形，其面积为，

因为平面，所以，

所以是直角三角形，其面积为，

同理的面积为， 面积为.  所以三棱锥的表面积为.

解: (1)证明：根据正方体的性质，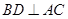

因为，

所以，又，所以，，

所以^.               ………………4分

(2)证明：连接，因为，

所以为平行四边形，因此，

由于是线段的中点，所以，      …………6分

因为面，平面，所以∥平面.   ……………8分

(3)是边长为的正三角形，其面积为，

因为平面，所以，

所以是直角三角形，其面积为，

同理的面积为，              ……………………10分

面积为.          所以三棱锥的表面积为