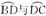摘要：(Ⅰ)证明:连结A1C.AC.AC和BD交于O.连结C1O．
网址：http://m.1010jiajiao.com/timu_id_425203[举报]
如图，已知半径为r的圆M的内接四边形ABCD的对角线AC和BD相互垂直且交点为P．
（1）若四边形ABCD中的一条对角线AC的长度为d（0＜d＜2r），试求：四边形ABCD面积的最大值；
（2）试探究：当点P运动到什么位置时，四边形ABCD的面积取得最大值，最大值为多少？
（3）对于之前小题的研究结论，我们可以将其类比到椭圆的情形．如图2，设平面直角坐标系中，已知椭圆Γ：
+
=1（a＞b＞0）的内接四边形ABCD的对角线AC和BD相互垂直且交于点P．试提出一个由类比获得的猜想，并尝试给予证明或反例否定．
查看习题详情和答案>>
（1）若四边形ABCD中的一条对角线AC的长度为d（0＜d＜2r），试求：四边形ABCD面积的最大值；
（2）试探究：当点P运动到什么位置时，四边形ABCD的面积取得最大值，最大值为多少？
（3）对于之前小题的研究结论，我们可以将其类比到椭圆的情形．如图2，设平面直角坐标系中，已知椭圆Γ：
| x2 |
| a2 |
| y2 |
| b2 |
已知四棱锥P-ABCD的底面是边长为4的正方形，PD⊥底面ABCD，PD=6，M，N分别为PB，AB的中点，设AC和BD相交于点O
（Ⅰ）证明：OM∥底面PAD；
（Ⅱ）若DF⊥PA且交PA于F点，证明DF⊥平面PAB；
（Ⅲ）求四面体D-MNB的体积 查看习题详情和答案>>
（Ⅰ）证明：OM∥底面PAD；
（Ⅱ）若DF⊥PA且交PA于F点，证明DF⊥平面PAB；
（Ⅲ）求四面体D-MNB的体积 查看习题详情和答案>>
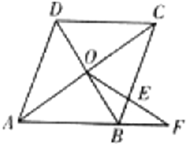
选做题：请考生在下列两题中任选一题作答，若两题都做，则按所做的第一题评阅计分．（1）（几何证明选讲选做题） 如图，平行四边形ABCD的对角线AC和BD交于点O，OE与BC和AB的延长线分别交于点E和F，若AB=2，BC=3，BF=1，则BE=
| 3 |
| 4 |
| 3 |
| 4 |
（2）（坐标系与参数方程选做题） 若直线l1：
|
与直线l2：
|
-1
-1
．
（理）已知函数f(x)=| ln(2-x2) |
| |x+2|-2 |
（1）试判断f（x）的奇偶性并给予证明；
（2）求证：f（x）在区间（0，1）单调递减；
（3）如图给出的是与函数f（x）相关的一个程序框图，试构造一个公差不为零的等差数列
{an}，使得该程序能正常运行且输出的结果恰好为0．请说明你的理由．
（文）如图，在平面直角坐标系中，方程为x2+y2+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直，且AC和BD分别在x轴和y轴上．
（1）求证：F＜0；
（2）若四边形ABCD的面积为8，对角线AC的长为2，且
| AB |
| AD |
（3）设四边形ABCD的一条边CD的中点为G，OH⊥AB且垂足为H．试用平面解析几何的研究方法判
断点O、G、H是否共线，并说明理由． 查看习题详情和答案>>
的弧长之比为1∶2.