如图，在矩形ABCD中，AB=

3

，BC=a，又PA⊥平面ABCD，PA=4．
（1）若在边BC上存在点Q，且使得PQ⊥QD，求a的取值范围；
（2）当BC边上存在唯一点Q，使PQ⊥QD时，求异面直线AQ与PD所成角的大小．

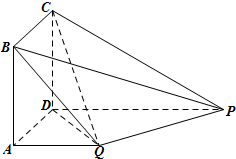如图，四边形ABCD为正方形，在四边形ADPQ中，PD∥QA．又QA⊥平面ABCD，QA=AB=

1

2

PD．
（1）证明：PQ⊥平面DCQ；
（2）CP上是否存在一点R，使QR∥平面ABCD，若存在，请求出R的位置，若不存在，请说明理由．

（2013•海淀区一模）在四棱锥P-ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC与BD的交点M恰好是AC中点，又∠CAD=30°，PA=AB=4，点N在线段PB上，且

PN

NB

=

1

3

．
（Ⅰ）求证：BD⊥PC；
（Ⅱ）求证：MN∥平面PDC；
（Ⅲ）设平面PAB∩平面PCD=l，试问直线l是否与直线CD平行，请说明理由．

如图，在△ABC中，O在AB上，且OB=OC=

2

3

AB，又PO⊥平面ABC，DA∥PO，DA=AO=

1

2

PO．
（Ⅰ）求证：PB∥平面COD；
（Ⅱ）求证：平面POD⊥平面COD．