题目内容
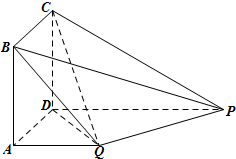 如图,四边形ABCD为正方形,在四边形ADPQ中,PD∥QA.又QA⊥平面ABCD,QA=AB=
如图,四边形ABCD为正方形,在四边形ADPQ中,PD∥QA.又QA⊥平面ABCD,QA=AB=| 1 | 2 |
(1)证明:PQ⊥平面DCQ;
(2)CP上是否存在一点R,使QR∥平面ABCD,若存在,请求出R的位置,若不存在,请说明理由.
分析:(1)要证明线面垂直PQ⊥平面DCQ,根据其判定定理,需要证明PQ垂直于平面DCQ内的两条相交直线,由已知可证明CD⊥PQ,只要再证明PQ⊥DQ即可.
(2)只要分别取PC、CD的中点,再利用三角形的中位线和平行四边形的判定与性质即可得到结论.
(2)只要分别取PC、CD的中点,再利用三角形的中位线和平行四边形的判定与性质即可得到结论.
解答:解: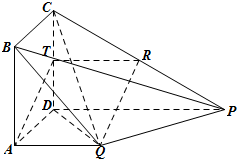 (1)法一:∵QA⊥平面ABCD,∴QA⊥CD,
(1)法一:∵QA⊥平面ABCD,∴QA⊥CD,
由四边形ABCD为正方形知DC⊥AD,
又QA、AD为平面PDAQ内两条相交直线,∴CD⊥平面PDAQ,∴CD⊥PQ.
在直角梯形PDAQ中可得DQ=PQ=
PD,∴PQ2+DQ2=PD2.
由勾股定理得逆定理得:PQ⊥QD.
又CD、QD为平面ADCB内两条相交直线,∴PQ⊥平面DCQ.
法二:∵QA⊥平面ABCD,QA?平面PDAQ,∴平面PDAQ⊥平面ABCD,交线为AD.
又四边形ABCD为正方形,DC⊥AD,∴DC⊥平面PDAQ,可得PQ⊥DC.
在直角梯形PDAQ中可得DQ=PQ=
PD,则PQ⊥QD.
又CD、QD为平面ADCB内两条相交直线,
∴PQ⊥平面DCQ.
(2)存在CP中点R,使QR∥平面ABCD.
证:取CD中点T,连接QR,RT,AT,由三角形的中位线定理得:RT∥DP,且RT=
DP,
又AQ∥DP,且AQ=
DP,从而AQ∥RT,且AQ=RT,
∴四边形AQRT为平行四边形,所以AT∥QR.
∵QR?平面ABCD,AT?平面ABCD,
∴QR∥平面ABCD.
即存在CP中点R,使QR∥平面ABCD
 (1)法一:∵QA⊥平面ABCD,∴QA⊥CD,
(1)法一:∵QA⊥平面ABCD,∴QA⊥CD,由四边形ABCD为正方形知DC⊥AD,
又QA、AD为平面PDAQ内两条相交直线,∴CD⊥平面PDAQ,∴CD⊥PQ.
在直角梯形PDAQ中可得DQ=PQ=
| ||
| 2 |
由勾股定理得逆定理得:PQ⊥QD.
又CD、QD为平面ADCB内两条相交直线,∴PQ⊥平面DCQ.
法二:∵QA⊥平面ABCD,QA?平面PDAQ,∴平面PDAQ⊥平面ABCD,交线为AD.
又四边形ABCD为正方形,DC⊥AD,∴DC⊥平面PDAQ,可得PQ⊥DC.
在直角梯形PDAQ中可得DQ=PQ=
| ||
| 2 |
又CD、QD为平面ADCB内两条相交直线,
∴PQ⊥平面DCQ.
(2)存在CP中点R,使QR∥平面ABCD.
证:取CD中点T,连接QR,RT,AT,由三角形的中位线定理得:RT∥DP,且RT=
| 1 |
| 2 |
又AQ∥DP,且AQ=
| 1 |
| 2 |
∴四边形AQRT为平行四边形,所以AT∥QR.
∵QR?平面ABCD,AT?平面ABCD,
∴QR∥平面ABCD.
即存在CP中点R,使QR∥平面ABCD
点评:掌握线面、面面平行和垂直的判定与性质定理是解题的关键.

练习册系列答案
相关题目
 如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD.
如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD. 如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB= 如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点.
如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点. 如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD
如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD
 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=